|
[VW, S & B: 2.6]
Observation leads to the following two assertions:
- There exists for every system a property called energy,
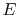 .
The system energy can be considered as a sum of internal energy,
kinetic energy, potential energy, and chemical energy.
.
The system energy can be considered as a sum of internal energy,
kinetic energy, potential energy, and chemical energy.
- Like the Zeroth Law, which defined a useful property, ``temperature,'' the First Law
defines a useful property called ``energy.''
- The two new terms (compared to what you have seen in physics and
dynamics, for example) are the internal energy and the chemical
energy. For most situations in this class, we will neglect the
chemical energy. We will generally not, however, neglect the
internal energy,
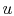 . It arises from the random or disorganized
motion of molecules in the system, as shown in
Figure 2.1. Since this molecular motion is
primarily a function of temperature, the internal energy is
sometimes called ``thermal energy.''
. It arises from the random or disorganized
motion of molecules in the system, as shown in
Figure 2.1. Since this molecular motion is
primarily a function of temperature, the internal energy is
sometimes called ``thermal energy.''
Figure 2.1:
Random motion is the physical basis for internal energy
|
|
The internal energy, 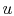 , is a function of the state of the system.
Thus
, is a function of the state of the system.
Thus
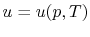 , or
, or
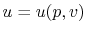 , or
, or
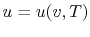 . Recall that
for pure substances the entire state of the system is specified if
any two properties are specified. (We will discuss the
equations that relate the internal energy to these other variables
as the course progresses.)
. Recall that
for pure substances the entire state of the system is specified if
any two properties are specified. (We will discuss the
equations that relate the internal energy to these other variables
as the course progresses.)
- The change in energy of a system is equal to the difference between
the heat added to the system and the work done by the
system,
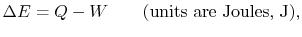 |
(2..1) |
where
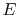 is the energy of the system,
is the energy of the system,
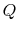 is the heat input to the system, and
is the heat input to the system, and
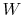 is the work done by the system.
is the work done by the system.
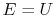 (thermal energy) +
(thermal energy) +
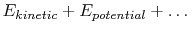
- Like the Zeroth Law, the First Law describes
the behavior of the new property [VW, S& B: Chapter 5].
- The equation can also be written on a per unit
mass basis
- In many situations the potential energy, kinetic energy, and chemical energy of
the system are constant or not important. Then
and
- Note that
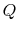 and
and 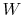 are not functions of
state, but
are not functions of
state, but 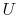 , which arises from molecular motion (see above),
depends only on the state of the system;
, which arises from molecular motion (see above),
depends only on the state of the system; 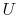 does not depend on how
the system got to that state. We therefore have the striking result
that:
does not depend on how
the system got to that state. We therefore have the striking result
that:
Sometimes this difference is emphasized by writing the
First Law in differential form,
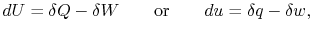 |
(2..2) |
where the symbol ``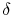 '' is used to denote that these are not
exact differentials but rather are dependent on path.
'' is used to denote that these are not
exact differentials but rather are dependent on path.
- Note that the signs are important:
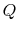 is defined to be positive if it is transferred to the
system; thus the numerical value we substitute for
is defined to be positive if it is transferred to the
system; thus the numerical value we substitute for 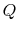 will be
positive if heat is transferred to the system from the
surroundings, and negative if heat is transferred from the
system to the surroundings. [VW, S
& B: 4.7-4.8]
will be
positive if heat is transferred to the system from the
surroundings, and negative if heat is transferred from the
system to the surroundings. [VW, S
& B: 4.7-4.8]
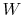 is defined to be positive if it is done by the system (see
Section 1.3); thus the numerical value we substitute
for
is defined to be positive if it is done by the system (see
Section 1.3); thus the numerical value we substitute
for 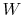 will be positive if the system is doing work, and
negative if work is being done on the system. [VW, S& B:
4.1-4.4]
will be positive if the system is doing work, and
negative if work is being done on the system. [VW, S& B:
4.1-4.4]
- For quasi-static processes we can substitute
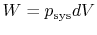 ,
,
To give an example of where the first law is applied, consider the
device shown in Figure 2.2. We heat a gas, it
expands against a weight, some force (pressure times area) is
applied over a distance, and work is done. The change in energy of
the system supplies the connection between the heat added and work
done. We will spend most of the course dealing with various
applications of the first law -- in one form or another.
Figure 2.2:
The change in energy of a system
relates the heat added to the work done
|
|
The form of the first law we have given here is sometimes called the
``control mass'' form, because it is well suited to dealing with
systems of a fixed mass. We will see in Section 2.5
that this form can be written for a control volume with mass flow in
and mass flow out (like a jet engine for example). We will call this
the ``control volume'' form of the first law [VW, S
& B: 5.8-5.12].
Muddy Points
What are the conventions for work and heat in the first law? (MP
2.1)
When does
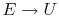 ? (MP 2.2)
? (MP 2.2)
Douglas Quattrochi
2006-08-06
|

