6.6 Entropy and Unavailable Energy (Lost Work by Another Name)
Consider a system consisting of a heat reservoir at 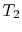 in
surroundings (the atmosphere) at
in
surroundings (the atmosphere) at 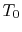 . The surroundings are
equivalent to a second reservoir at
. The surroundings are
equivalent to a second reservoir at 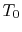 . For an amount of heat,
. For an amount of heat,
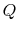 , transferred from the reservoir, the maximum work we could
derive is
, transferred from the reservoir, the maximum work we could
derive is 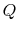 times the thermal efficiency of a Carnot cycle
operated between these two temperatures:
times the thermal efficiency of a Carnot cycle
operated between these two temperatures:
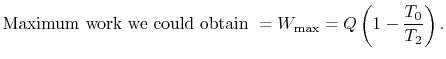 |
(6..7) |
Only part of the heat transferred can be turned into work, in other
words only part of the heat energy is available to be used as
work.
Suppose we transferred the same amount of heat from the reservoir
directly to another reservoir at a temperature 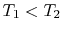 . The
maximum work available from the quantity of heat,
. The
maximum work available from the quantity of heat, 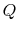 , before
the transfer to the reservoir at
, before
the transfer to the reservoir at 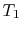 is
is
The maximum amount
of work available after the transfer to the reservoir at
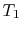 is
is
There is an amount of energy that could have been
converted to work prior to the irreversible heat transfer process of
magnitude 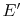 ,
,
However, 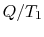 is the entropy gain of the reservoir at
is the entropy gain of the reservoir at 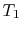 and
(
and
(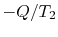 ) is the entropy decrease of the reservoir at
) is the entropy decrease of the reservoir at 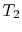 . The
amount of energy,
. The
amount of energy, 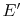 , that could have been converted to work (but
now cannot be) can therefore be written in terms of entropy changes
and the temperature of the surroundings as
, that could have been converted to work (but
now cannot be) can therefore be written in terms of entropy changes
and the temperature of the surroundings as
The situation just described is a special case of an important
principle concerning entropy changes, irreversibility and the loss
of capability to do work. We thus now develop it in a more general
fashion, considering an arbitrary system undergoing an irreversible
state change, which transfers heat to the surroundings (for example
the atmosphere), which can be assumed to be at constant temperature,
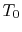 . The change in internal energy of the system during the state
change is
. The change in internal energy of the system during the state
change is
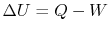 . The change in entropy of the
surroundings is (with
. The change in entropy of the
surroundings is (with 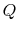 the heat transfer to the system)
the heat transfer to the system)
Now consider restoring the system to the initial state by a
reversible process. To do this we need to do work,
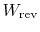 ,
on the system and extract from the system a quantity
of heat,
,
on the system and extract from the system a quantity
of heat,
 . (We did this, for example, in ``undoing''
the free expansion process.) The change in internal energy is (with
the quantities
. (We did this, for example, in ``undoing''
the free expansion process.) The change in internal energy is (with
the quantities
 and
and
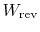 both regarded,
in this example, as positive for work done by the
surroundings and heat given to the surroundings)6.2.
both regarded,
in this example, as positive for work done by the
surroundings and heat given to the surroundings)6.2.
In this reversible process, the entropy of the surroundings is
changed by
For the combined changes (the irreversible state change and the
reversible state change back to the initial state), the energy
change is zero because the energy is a function of state,
Thus,
For the system, the overall entropy change for the combined process
is zero, because the entropy is a function of state,
The total entropy
change is thus only reflected in the entropy change of the
surroundings:
The surroundings can be considered a constant temperature heat
reservoir and their entropy change is given by
We also know that the total entropy change, for system plus
surroundings is,
The total entropy change is associated only with the
irreversible process and is related to the work in the two processes
by
The quantity
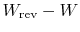 represents the extra work
required to restore the system to the original state. If the process
were reversible, we would not have needed any extra work to
do this. It represents a quantity of work that is now unavailable
because of the irreversibility. The quantity
represents the extra work
required to restore the system to the original state. If the process
were reversible, we would not have needed any extra work to
do this. It represents a quantity of work that is now unavailable
because of the irreversibility. The quantity
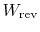 can
also be interpreted as the work that the system would have done if
the original process were reversible. From either of these
perspectives we can identify
can
also be interpreted as the work that the system would have done if
the original process were reversible. From either of these
perspectives we can identify
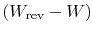 as the quantity
we denoted previously as
as the quantity
we denoted previously as 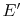 , representing lost work. The lost work
in any irreversible process can therefore be related to the total
entropy change (system plus surroundings) and the temperature of the
surroundings by
, representing lost work. The lost work
in any irreversible process can therefore be related to the total
entropy change (system plus surroundings) and the temperature of the
surroundings by
To summarize the results of the above arguments for processes where
heat can be exchanged with the surroundings at 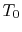 :
:
-
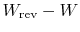 represents the difference between work we actually obtained
and work that would be done during a reversible state change. It is
the extra work that would be needed to restore the system to its
initial state.
represents the difference between work we actually obtained
and work that would be done during a reversible state change. It is
the extra work that would be needed to restore the system to its
initial state.
- For a reversible process,
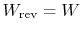 ;
;
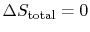 .
.
- For an irreversible process,
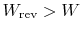 ;
;
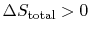 .
.
-
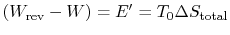 is the energy that becomes unavailable for work during an
irreversible process.
is the energy that becomes unavailable for work during an
irreversible process.
Muddy Points
Is 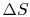 path dependent? (MP 6.11)
path dependent? (MP 6.11)
Are
 and
and
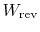 the
the 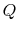 and
and 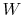 going from
the final state back to the initial state?
(MP 6.12)
going from
the final state back to the initial state?
(MP 6.12)
Douglas Quattrochi
2006-08-06
|


![$\displaystyle = Q\left[\left(1-\frac{T_0}{T_2}\right)-\left(1-\frac{T_0}{T_1}\right)\right] =Q\left[\frac{T_0}{T_1}-\frac{T_0}{T_2}\right],$](img741.png)
![$\displaystyle = T_0\left[\frac{Q}{T_1}-\frac{Q}{T_2}\right].$](img742.png)
![]() . The change in internal energy of the system during the state
change is
. The change in internal energy of the system during the state
change is
![]() . The change in entropy of the
surroundings is (with
. The change in entropy of the
surroundings is (with ![]() the heat transfer to the system)
the heat transfer to the system)


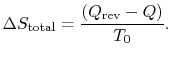
![$\displaystyle \Delta S_\textrm{total} = \left[\Delta S_\textrm{irreversible pro...
...{\Delta S}_\textrm{reversible process}\right]_\textrm{system and
surroundings}.$](img759.png)
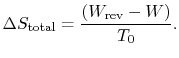
![]() :
:
![]() path dependent? (MP 6.11)
path dependent? (MP 6.11)
![]() and
and
![]() the
the ![]() and
and ![]() going from
the final state back to the initial state?
(MP 6.12)
going from
the final state back to the initial state?
(MP 6.12)