7.2 Microscopic and Macroscopic Descriptions of a System
The microscopic description of a system is the complete
description of each particle in this system. In the above example,
the microscopic description of the gas would be the list of the
state of each molecule: position and velocity in this problem. It
would require a great deal of data for this description; there are
roughly 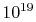 molecules in a cube of air one centimeter on a
side at room temperature and pressure. The macroscopic
description, which is in terms of a few (two!) properties is thus
far more accessible and useable for engineering applications,
although it is restricted to equilibrium states.
molecules in a cube of air one centimeter on a
side at room temperature and pressure. The macroscopic
description, which is in terms of a few (two!) properties is thus
far more accessible and useable for engineering applications,
although it is restricted to equilibrium states.
To address the description of entropy on a microscopic level, we
need to state some results concerning microscopic systems. These
results and the computations and arguments below are taken almost
entirely from the excellent discussion in Chapter 6 of
Engineering Thermodynamics by Reynolds and
Perkins7.1.
For a given macroscopic system, there are many microscopic states. A
key idea from quantum mechanics is that the states of atoms,
molecules, and entire systems are discretely quantized. This means
that a system of particles under certain constraints, like being in
a box of a specified size, or having a fixed total energy, can exist
in a finite number of allowed microscopic states. This number can be
very big, but it is finite. The microstates of the system keep
changing with time from one quantum state to another as molecules
move and collide with one another. The probability for the system to
be in a particular quantum state is defined by its quantum-state
probability 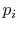 . The set of the
. The set of the 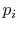 is called the distribution
of probability. The sum of the probabilities of all the allowed
quantum states must be unity, hence for any time
is called the distribution
of probability. The sum of the probabilities of all the allowed
quantum states must be unity, hence for any time 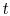 ,
,
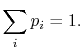 |
(7..2) |
When the system reaches equilibrium, the individual molecules still
change from one quantum state to another. In equilibrium, however,
the system state does not change with time; so the probabilities for
the different quantum states are independent of time. This
distribution is then called the equilibrium distribution, and the
probability 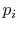 can be viewed as the fraction of time a system
spends in the
can be viewed as the fraction of time a system
spends in the
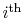 quantum state. In what follows, we
limit consideration to equilibrium states.
quantum state. In what follows, we
limit consideration to equilibrium states.
We can get back to macroscopic quantities from the microscopic
description using the probability distribution. For instance, the
macroscopic energy of the system would be the weighted average of
the successive energies of the system (the energies of the quantum
states); the energies are weighted by the relative time the system
spends in the corresponding microstates. In terms of probabilities,
the average energy,
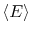 , is
, is
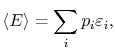 |
(7..3) |
where
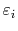 is the energy of a quantum state.
is the energy of a quantum state.
The probability distribution provides information on the randomness of the equilibrium quantum
states. For example, suppose the system can only exist in three states (1, 2 and 3). If the
distribution probability is
the system is in quantum state 1 and there is no randomness. If we
were asked what quantum state the system is in, we would be able to
say it is always in state 1. If the distribution were
the randomness would not be zero and would be equal in both cases.
We would be more uncertain about the instantaneous quantum state
than in the first situation.
Maximum randomness corresponds to the case where the three states
are equally probable:
In this case, we can only guess the instantaneous state with 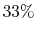 probability.
probability.
UnifiedTP
| 
