12.3 The Euler Turbine Equation
The Euler turbine equation relates the power added to or removed
from the flow, to characteristics of a rotating blade row. The
equation is based on the concepts of conservation of angular
momentum and conservation of energy. We will work with the model of
the blade row shown in Figure 12.2.
Figure 12.2:
Control volume for
Euler Turbine Equation.
|
|
Applying conservation of angular momentum, we note that the torque,
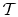 , must be equal to the time rate of change of angular
momentum in a streamtube that flows through the device
, must be equal to the time rate of change of angular
momentum in a streamtube that flows through the device
This is true whether the blade row is rotating or not. The sign
matters (i.e. angular momentum is a vector - positive means it is
spinning in one direction, negative means it is spinning in the
other direction). So depending on how things are defined, there can
be positive and negative torques, and positive and negative angular
momentum. In Figure 9.2, torque is positive when
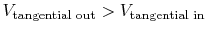 -- the
same sense as the angular velocity.
-- the
same sense as the angular velocity.
If the
blade row is moving, then work is done on/by the fluid. The work per
unit time, or power,  , is the torque multiplied by the angular
velocity,
, is the torque multiplied by the angular
velocity,  :
:
If torque and
angular velocity are of like sign, work is being done on the fluid
(a compressor). If torque and angular velocity are of opposite sign
work is being extracted from the fluid (a turbine). Here is another
approach to the same idea:
- If the tangential velocity increases
across a blade row (where positive tangential velocity is defined in
the same direction as the rotor motion) then work is added to the
flow (this happens in a compressor).
- If the tangential velocity decreases across a
blade row (where positive tangential velocity is defined in the same
direction as the rotor motion) then work is removed from the flow
(this happens in a
turbine).
From the steady flow energy equation,
with
Then
equating this expression of conservation of energy with our
expression from conservation of angular momentum, we arrive at:
or for a perfect gas with
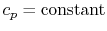 ,
,
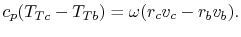 |
(12..3) |
Equation (12.3) is called the Euler Turbine
Equation. It relates the temperature ratio (and hence the pressure
ratio) across a turbine or compressor to the rotational speed and
the change in
momentum per unit mass. Note that the velocities used in this
equation are what we will later call absolute frame velocities (as
opposed to relative frame velocities).
- If angular momentum
increases across a blade row, then
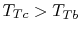 and work was done on
the fluid (a compressor).
and work was done on
the fluid (a compressor).
- If angular momentum decreases across a
blade row, then
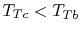 and work was done by the fluid (a
turbine).
and work was done by the fluid (a
turbine).
UnifiedTP
|


![]() , is the torque multiplied by the angular
velocity,
, is the torque multiplied by the angular
velocity, ![]() :
: