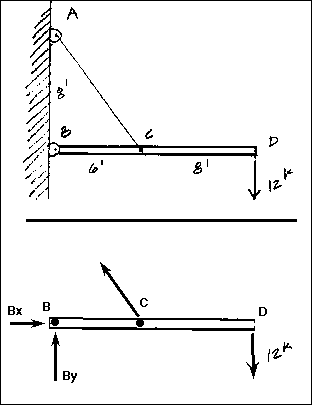
Solution:
a. The free body diagram of the horizontal member will include the 12k force at D and the reactions at B and C. The pinned support at B will have a horizontal and a vertical component although the angle at which the total force B acts is unknown at this point. The direction of C is already known because it must act in the direction of the wire. Hoever, it is more easily solved when it is broken into rectangular components.
b. Apply the familiar equations of static equilibrium to algebraicly solve for the reactions at B and C.
Sum Fx = 0 = Bx + CxSolve for Cy using the moment equation:
Sum Fy = 0 = -12k + By + Cy
Sum MB = 0 = -Cy(6ft) + 12k(14ft)
6Cy = 168kftSolve for By using Cy in Sum Fy = 0:
Cy = 28k
-By = -12k + 28kNow there are two more unknowns, Bx and Cx, but only one other equation. However, it can be seen that C is part of a 3-4-5 triangle. Using this information, solve for C and Cx:
-By = 16k
By = -16k
Cy = 28k = 4/5 CNow solve for Bx:
C = 35k
Cx = -3/5 (35k)
Cx = -21k
Bx = -CxFinally, solve for B using the Pythagorean Theorem:
Bx = 21k
B = SQRT (21k^2 + (-16k)^2) = SQRT (256) = 16k acting down and to the rightThe angle for the reaction at B would be:
ø = arctan (-16 / 21)
ø = 37.3 degrees below the x axis
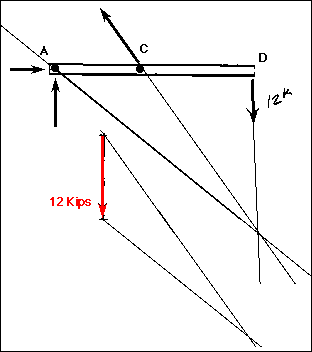
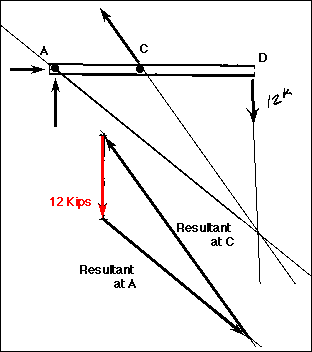
Now, extend the lines of action of the two forces that have a known direction until they intersect. This is the point of origin for the three-force system. It is a VERY important point! Now, the line of action and the direction of the reaction at B can be found by simply drawing a vector from point B to the point of origin. This is the line of action of the reaction force. The direction of the resulting third force is also known when inspection determines the kind of force that must be applied to put the system into equilibrium. The magnitude of B and C can be found using the triangle method and making assumptions about the sense of the forces.