Reading 13: Abstraction Functions & Rep Invariants
Software in 6.005
| Safe from bugs | Easy to understand | Ready for change |
|---|---|---|
| Correct today and correct in the unknown future. | Communicating clearly with future programmers, including future you. | Designed to accommodate change without rewriting. |
Objectives
Today’s reading introduces several ideas:
- invariants
- representation exposure
- abstraction functions
- representation invariants
In this reading, we study a more formal mathematical idea of what it means for a class to implement an ADT, via the notions of abstraction functions and rep invariants. These mathematical notions are eminently practical in software design. The abstraction function will give us a way to cleanly define the equality operation on an abstract data type (which we’ll discuss in more depth in a future class). The rep invariant will make it easier to catch bugs caused by a corrupted data structure.
Invariants
Resuming our discussion of what makes a good abstract data type, the final, and perhaps most important, property of a good abstract data type is that it preserves its own invariants. An invariant is a property of a program that is always true, for every possible runtime state of the program. Immutability is one crucial invariant that we’ve already encountered: once created, an immutable object should always represent the same value, for its entire lifetime. Saying that the ADT preserves its own invariants means that the ADT is responsible for ensuring that its own invariants hold. It doesn’t depend on good behavior from its clients.
When an ADT preserves its own invariants, reasoning about the code becomes much easier. If you can count on the fact that Strings never change, you can rule out that possibility when you’re debugging code that uses Strings – or when you’re trying to establish an invariant for another ADT that uses Strings. Contrast that with a string type that guarantees that it will be immutable only if its clients promise not to change it. Then you’d have to check all the places in the code where the string might be used.
Immutability
Later in this reading, we’ll see many interesting invariants. Let’s focus on immutability for now. Here’s a specific example:
/**
* This immutable data type represents a tweet from Twitter.
*/
public class Tweet {
public String author;
public String text;
public Date timestamp;
/**
* Make a Tweet.
* @param author Twitter user who wrote the tweet.
* @param text text of the tweet
* @param timestamp date/time when the tweet was sent
*/
public Tweet(String author, String text, Date timestamp) {
this.author = author;
this.text = text;
this.timestamp = timestamp;
}
}How do we guarantee that these Tweet objects are immutable – that, once a tweet is created, its author, message, and date can never be changed?
The first threat to immutability comes from the fact that clients can — in fact must — directly access its fields. So nothing’s stopping us from writing code like this:
Tweet t = new Tweet("justinbieber",
"Thanks to all those beliebers out there inspiring me every day",
new Date());
t.author = "rbmllr";This is a trivial example of representation exposure, meaning that code outside the class can modify the representation directly. Rep exposure like this threatens not only invariants, but also representation independence. We can’t change the implementation of Tweet without affecting all the clients who are directly accessing those fields.
Fortunately, Java gives us language mechanisms to deal with this kind of rep exposure:
public class Tweet {
private final String author;
private final String text;
private final Date timestamp;
public Tweet(String author, String text, Date timestamp) {
this.author = author;
this.text = text;
this.timestamp = timestamp;
}
/** @return Twitter user who wrote the tweet */
public String getAuthor() {
return author;
}
/** @return text of the tweet */
public String getText() {
return text;
}
/** @return date/time when the tweet was sent */
public Date getTimestamp() {
return timestamp;
}
}The private and public keywords indicate which fields and methods are accessible only within the class and which can be accessed from outside the class.
The final keyword also helps by guaranteeing that the fields of this immutable type won’t be reassigned after the object is constructed.
But that’s not the end of the story: the rep is still exposed! Consider this perfectly reasonable client code that uses Tweet:
/** @return a tweet that retweets t, one hour later*/
public static Tweet retweetLater(Tweet t) {
Date d = t.getTimestamp();
d.setHours(d.getHours()+1);
return new Tweet("rbmllr", t.getText(), d);
}retweetLater takes a tweet and should return another tweet with the same message (called a retweet) but sent an hour later. The retweetLater method might be part of a system that automatically echoes funny things that Twitter celebrities say.
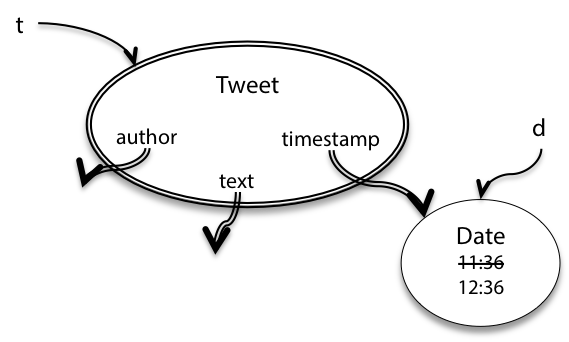
What’s the problem here? The getTimestamp call returns a reference to the same date object referenced by tweet t.
t.timestamp and d are aliases to the same mutable object. So when that date object is mutated by d.setHours(), this affects the date in t as well, as shown in the snapshot diagram.
Tweet’s immutability invariant has been broken. The problem is that Tweet leaked out a reference to a mutable object that its immutability depended on. We exposed the rep, in such a way that Tweet can no longer guarantee that its objects are immutable. Perfectly reasonable client code created a subtle bug.
We can patch this kind of rep exposure by using defensive copying: making a copy of a mutable object to avoid leaking out references to the rep. Here’s the code:
public Date getTimestamp() {
return new Date(Date.getTime());
}Mutable types often have a copy constructor that allows you to make a new instance that duplicates the value of an existing instance.
In this case, Date’s copy constructor uses the timestamp value, measured in milliseconds since January 1, 1970. As another example, StringBuilder’s copy constructor takes a String. Another way to copy a mutable object is clone(), which is supported by some types but not all.
There are unfortunate problems with the way clone() works in Java.
For more, see Josh Bloch, Effective Java, item 11.
So we’ve done some defensive copying in the return value of getTimestamp.
But we’re not done yet! There’s still rep exposure. Consider this (again perfectly reasonable) client code:
/** @return a list of 24 inspiring tweets, one per hour today */
public static List<Tweet> tweetEveryHourToday () {
List<Tweet> list = new ArrayList<Tweet>();
Date date = new Date();
for (int i=0; i < 24; i++) {
date.setHours(i);
list.add(new Tweet("rbmllr", "keep it up! you can do it", date));
}
return list;
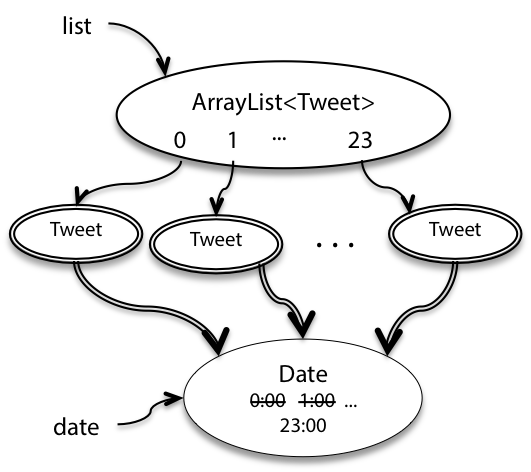
}This code intends to advance a single Date object through the 24 hours of a day, creating a tweet for every hour. But notice that the constructor of Tweet saves the reference that was passed in, so all 24 Tweet objects end up with the same time, as shown in this snapshot diagram.
Again, the immutability of Tweet has been violated. We can fix this problem too by using judicious defensive copying, this time in the constructor:
public Tweet(String author, String text, Date timestamp) {
this.author = author;
this.text = text;
this.timestamp = new Date(timestamp.getTime());
}In general, you should carefully inspect the argument types and return types of all your ADT operations. If any of the types are mutable, make sure your implementation doesn’t return direct references to its representation. Doing that creates rep exposure.
You may object that this seems wasteful. Why make all these copies of dates? Why can’t we just solve this problem by a carefully written specification, like this?
/**
* Make a Tweet.
* @param author Twitter user who wrote the tweet.
* @param text text of the tweet
* @param timestamp date/time when the tweet was sent. Caller must never
* mutate this Date object again!
*/
public Tweet(String author, String text, Date timestamp) {This approach is sometimes taken when there isn’t any other reasonable alternative – for example, when the mutable object is too large to copy efficiently. But the cost in your ability to reason about the program, and your ability to avoid bugs, is enormous. In the absence of compelling arguments to the contrary, it’s almost always worth it for an abstract data type to guarantee its own invariants, and preventing rep exposure is essential to that.
An even better solution is to prefer immutable types. If we had used an immutable date object, like java.time.ZonedDateTime, instead of the mutable java.util.Date, then we would have ended this section after talking about public and private. No further rep exposure would have been possible.
Immutable Wrappers Around Mutable Data Types
The Java collections classes offer an interesting compromise: immutable wrappers.
Collections.unmodifiableList() takes a (mutable) List and wraps it with an object that looks like a List, but whose mutators are disabled – set(), add(), remove() throw exceptions.
So you can construct a list using mutators, then seal it up in an unmodifiable wrapper (and throw away your reference to the original mutable list), and get an immutable list.
The downside here is that you get immutability at runtime, but not at compile time. Java won’t warn you at compile time if you try to sort() this unmodifiable list. You’ll just get an exception at runtime. But that’s still better than nothing, so using unmodifiable lists, maps, and sets can be a very good way to reduce the risk of bugs.
Reading exercises
Consider the following problematic datatype:
/** Represents an immutable right triangle. */
class RightTriangle {
/*A*/ private double[] sides;
// sides[0] and sides[1] are the two legs,
// and sides[2] is the hypotenuse, so declare it to avoid having a
// magic number in the code:
/*B*/ public static final int HYPOTENUSE = 2;
/** Make a right triangle.
* @param legA, legB the two legs of the triangle
* @param hypotenuse the hypotenuse of the triangle.
*C* * Requires hypotenuse^2 = legA^2 + legB^2
* (within the error tolerance of double arithmetic)
*/
public RightTriangle(double legA, double legB, double hypotenuse) {
/*D*/ this.sides = new double[] { legA, legB, hypotenuse };
}
/** Get all the sides of the triangle.
* @return three-element array with the triangle's side lengths
*/
public double[] getAllSides() {
/*E*/ return sides;
}
/** @return length of the triangle's hypotenuse */
public double getHypotenuse() {
return sides[HYPOTENUSE];
}
/** @param factor to multiply the sides by
* @return a triangle made from this triangle by
* multiplies all side lengths by factor.
*/
public RightTriangle scale(double factor) {
return new RightTriangle (sides[0]*factor, sides[1]*factor, sides[2]*factor);
}
/** @return a regular triangle made from this triangle.
* A regular right triangle is one in which
* both legs have the same length.
*/
public RightTriangle regularize() {
double bigLeg = Math.max(side[0], side[1]);
return new RightTriangle (bigLeg, bigLeg, side[2]);
}
}(missing explanation)
(missing explanation)
(missing explanation)
(missing explanation)
(missing explanation)
Rep Invariant and Abstraction Function
We now take a deeper look at the theory underlying abstract data types. This theory is not only elegant and interesting in its own right; it also has immediate practical application to the design and implementation of abstract types. If you understand the theory deeply, you’ll be able to build better abstract types, and will be less likely to fall into subtle traps.
In thinking about an abstract type, it helps to consider the relationship between two spaces of values.
The space of representation values (or rep values for short) consists of the values of the actual implementation entities. In simple cases, an abstract type will be implemented as a single object, but more commonly a small network of objects is needed, so this value is actually often something rather complicated. For now, though, it will suffice to view it simply as a mathematical value.
The space of abstract values consists of the values that the type is designed to support. These are a figment of our imaginations. They’re platonic entities that don’t exist as described, but they are the way we want to view the elements of the abstract type, as clients of the type. For example, an abstract type for unbounded integers might have the mathematical integers as its abstract value space; the fact that it might be implemented as an array of primitive (bounded) integers, say, is not relevant to the user of the type.
Now of course the implementor of the abstract type must be interested in the representation values, since it is the implementor’s job to achieve the illusion of the abstract value space using the rep value space.
Suppose, for example, that we choose to use a string to represent a set of characters:
public class CharSet {
private String s;
...
}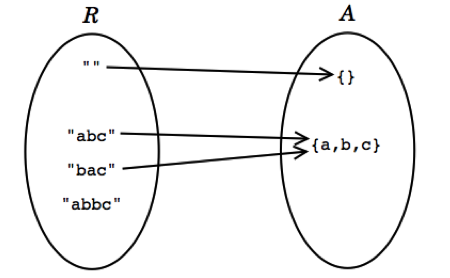
Then the rep space R contains Strings, and the abstract space A is mathematical sets of characters. We can show the two value spaces graphically, with an arc from a rep value to the abstract value it represents. There are several things to note about this picture:
- Every abstract value is mapped to by some rep value. The purpose of implementing the abstract type is to support operations on abstract values. Presumably, then, we will need to be able to create and manipulate all possible abstract values, and they must therefore be representable.
- Some abstract values are mapped to by more than one rep value. This happens because the representation isn’t a tight encoding. There’s more than one way to represent an unordered set of characters as a string.
- Not all rep values are mapped. In this case, the string “abbc” is not mapped. In this case, we have decided that the string should not contain duplicates. This will allow us to terminate the remove method when we hit the first instance of a particular character, since we know there can be at most one.
In practice, we can only illustrate a few elements of the two spaces and their relationships; the graph as a whole is infinite. So we describe it by giving two things:
1. An abstraction function that maps rep values to the abstract values they represent:
AF : R → A
The arcs in the diagram show the abstraction function. In the terminology of functions, the properties we discussed above can be expressed by saying that the function is surjective (also called onto), not necessarily bijective (also called one-to-one), and often partial.
2. A rep invariant that maps rep values to booleans:
RI : R → boolean
For a rep value r, RI(r) is true if and only if r is mapped by AF. In other words, RI tells us whether a given rep value is well-formed. Alternatively, you can think of RI as a set: it’s the subset of rep values on which AF is defined.
Both the rep invariant and the abstraction function should be documented in the code, right next to the declaration of the rep itself:
public class CharSet {
private String s;
// Rep invariant:
// s contains no repeated characters
// Abstraction Function:
// represents the set of characters found in s
...
}A common confusion about abstraction functions and rep invariants is that they are determined by the choice of rep and abstract value spaces, or even by the abstract value space alone. If this were the case, they would be of little use, since they would be saying something redundant that’s already available elsewhere.
The abstract value space alone doesn’t determine AF or RI: there can be several representations for the same abstract type. A set of characters could equally be represented as a string, as above, or as a bit vector, with one bit for each possible character. Clearly we need two different abstraction functions to map these two different rep value spaces.
It’s less obvious why the choice of both spaces doesn’t determine AF and RI. The key point is that defining a type for the rep, and thus choosing the values for the space of rep values, does not determine which of the rep values will be deemed to be legal, and of those that are legal, how they will be interpreted. Rather than deciding, as we did above, that the strings have no duplicates, we could instead allow duplicates, but at the same time require that the characters be sorted, appearing in nondecreasing order. This would allow us to perform a binary search on the string and thus check membership in logarithmic rather than linear time. Same rep value space – different rep invariant:
public class CharSet {
private String s;
// Rep invariant:
// s[0] <= s[1] <= ... <= s[s.length()-1]
// Abstraction Function:
// represents the set of characters found in s
...
}Even with the same type for the rep value space and the same rep invariant RI, we might still interpret the rep differently, with different abstraction functions AF. Suppose RI admits any string of characters. Then we could define AF, as above, to interpret the array’s elements as the elements of the set. But there’s no a priori reason to let the rep decide the interpretation. Perhaps we’ll interpret consecutive pairs of characters as subranges, so that the string rep “acgg” is interpreted as two range pairs, [a-c] and [g-g], and therefore represents the set {a,b,c,g}. Here’s what the AF and RI would look like for that representation:
public class CharSet {
private String s;
// Rep invariant:
// s.length is even
// s[0] <= s[1] <= ... <= s[s.length()-1]
// Abstraction Function:
// represents the union of the ranges
// {s[i]...s[i+1]} for each adjacent pair of characters
// in s
...
}The essential point is that designing an abstract type means not only choosing the two spaces – the abstract value space for the specification and the rep value space for the implementation – but also deciding what rep values to use and how to interpret them.
It’s critically important to write down these assumptions in your code, as we’ve done above, so that future programmers (and your future self) are aware of what the representation actually means. Why? What happens if different implementers disagree about the meaning of the rep?
Reading exercises
(missing explanation)
(missing explanation)
Suppose C is an abstract data type whose representation has two String fields:
class C {
private String s;
private String t;
...
}(missing explanation)
Suppose Louis Reasoner has created CharSet with the following rep:
public class CharSet {
private String s;
...
}But Louis unfortunately neglects to write down the abstraction function (AF) and rep invariant (RI). Here are four possible AF/RI pairs that might have been what Louis had in mind. All of them were also mentioned in the reading above.
SortedRep:
// AF: represents the set of characters found in s
// RI: s[0] < s[1] < ... < s[s.length()-1]SortedRangeRep:
// AF: represents the union of the ranges {s[i]...s[i+1]} for each adjacent pair of characters in s
// RI: s.length is even, and s[0] < s[1] < ... < s[s.length()-1]NoRepeatsRep:
// AF: represents the set of characters found in s
// RI: s contains no character more than onceAnyRep:
// AF: represents the set of characters found in s
// RI: trueLouis has three teammates helping him implement CharSet, each working on a different operation: add(), remove(), and contains().
Their implementations are below.
Which of the possible AF/RI pairs are consistent with each programmer’s implementation?
public void add(char c) {
s = s + c;
}(missing explanation)
public void remove(char c) {
int position = s.indexOf(c);
if (position >= 0) {
s = s.substring(0, position) + s.substring(position+1, s.length());
}
}(missing explanation)
public boolean contains(char c) {
for (int i = 0; i < s.length(); i += 2) {
char low = s.charAt(i);
char high = s.charAt(i+1);
if (low <= c && c <= high) {
return true;
}
}
return false;
}(missing explanation)
Example: Rational Numbers
Here’s an example of an abstract data type for rational numbers. Look closely at its rep invariant and abstraction function.
public class RatNum {
private final int numer;
private final int denom;
// Rep invariant:
// denom > 0
// numer/denom is in reduced form
// Abstraction Function:
// represents the rational number numer / denom
/** Make a new Ratnum == n. */
public RatNum(int n) {
numer = n;
denom = 1;
checkRep();
}
/**
* Make a new RatNum == (n / d).
* @param n numerator
* @param d denominator
* @throws ArithmeticException if d == 0
*/
public RatNum(int n, int d) throws ArithmeticException {
// reduce ratio to lowest terms
int g = gcd(n, d);
n = n / g;
d = d / g;
// make denominator positive
if (d < 0) {
numer = -n;
denom = -d;
} else {
numer = n;
denom = d;
}
checkRep();
}
}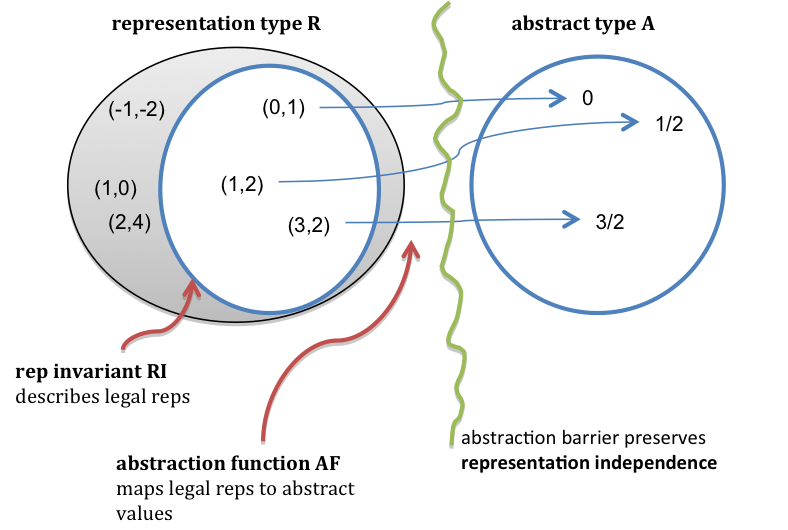
Here is a picture of the abstraction function and rep invariant for this code. The RI requires that numerator/denominator pairs be in reduced form (i.e., lowest terms), so pairs like (2,4) and (18,12) above should be drawn as outside the RI.
It would be completely reasonable to design another implementation of this same ADT with a more permissive RI. With such a change, some operations might become more expensive to perform, and others cheaper.
Checking the Rep Invariant
The rep invariant isn’t just a neat mathematical idea. If your implementation asserts the rep invariant at run time, then you can catch bugs early. Here’s a method for RatNum that tests its rep invariant:
// Check that the rep invariant is true
// *** Warning: this does nothing unless you turn on assertion checking
// by passing -enableassertions to Java
private void checkRep() {
assert denom > 0;
assert gcd(numer, denom) == 1;
}You should certainly call checkRep() to assert the rep invariant at the end of every operation that creates or mutates the rep – in other words, creators, producers, and mutators. Look back at the RatNum code above, and you’ll see that it calls checkRep() at the end of both constructors.
Observer methods don’t normally need to call checkRep(), but it’s good defensive practice to do so anyway. Why? Calling checkRep() in every method, including observers, means you’ll be more likely to catch rep invariant violations caused by rep exposure.
Why is checkRep private? Who should be responsible for checking and enforcing a rep invariant – clients, or the implementation itself?
No Null Values in the Rep
Recall from the specs reading that null values are troublesome and unsafe, so much so that we try to remove them from our programming entirely. In 6.005, the preconditions and postconditions of our methods implicitly require that objects and arrays be non-null.
We extend that prohibition to the reps of abstract data types. By default, in 6.005, the rep invariant implicitly includes x != null for every reference x in the rep that has object type (including references inside arrays or lists). So if your rep is:
class CharSet {
String s;
}then its rep invariant automatically includes s != null, and you don’t need to state it in a rep invariant comment.
When it’s time to implement that rep invariant in a checkRep() method, however, you still must implement the s != null check, and make sure that your checkRep() correctly fails when s is null. Often that check comes for free from Java, because checking other parts of your rep invariant will throw an exception if s is null. For example, if your checkRep() looks like this:
private void checkRep() {
assert s.length() % 2 == 0;
...
}then you don’t need assert s!= null, because the call to s.length() will fail just as effectively on a null reference. But if s is not otherwise checked by your rep invariant, then assert s != null explicitly.
Reading exercises
(missing explanation)
Documenting the AF, RI, and Safety from Rep Exposure
It’s good practice to document the abstraction function and rep invariant in the class, using comments right where the private fields of the rep are declared. We’ve been doing that above.
Another piece of documentation that 6.005 asks you to write is a rep exposure safety argument. This is a comment that examines each part of the rep, looks at the code that handles that part of the rep (particularly with respect to parameters and return values from clients, because that is where rep exposure occurs), and presents a reason why the code doesn’t expose the rep.
Here’s an example of Tweet with its rep invariant, abstraction function, and safety from rep exposure fully documented:
// Immutable type representing a tweet.
public class Tweet {
private final String author;
private final String text;
private final Date timestamp;
// Rep invariant:
// author is a Twitter username (a nonempty string of letters, digits, underscores)
// text.length <= 140
// Abstraction Function:
// represents a tweet posted by author, with content text, at time timestamp
// Safety from rep exposure:
// All fields are private;
// author and text are Strings, so are guaranteed immutable;
// timestamp is a mutable Date, so Tweet() constructor and getTimestamp()
// make defensive copies to avoid sharing the rep's Date object with clients.
// Operations (specs and method bodies omitted to save space)
public Tweet(String author, String text, Date timestamp) { ... }
public String getAuthor() { ... }
public String getText() { ... }
public Date getTimestamp() { ... }
}Notice that we don’t have any explicit rep invariant conditions on timestamp (aside from the conventional assumption that timestamp!=null, which we have for all object references). But we still need to include timestamp in the rep exposure safety argument, because the immutability property of the whole type depends on all the fields remaining unchanged.
Here are the arguments for RatNum.
// Immutable type representing a rational number.
public class RatNum {
private final int numer;
private final int denom;
// Rep invariant:
// denom > 0
// numer/denom is in reduced form, i.e. gcd(|numer|,denom) = 1
// Abstraction Function:
// represents the rational number numer / denom
// Safety from rep exposure:
// All fields are private, and all types in the rep are immutable.
// Operations (specs and method bodies omitted to save space)
public RatNum(int n) { ... }
public RatNum(int n, int d) throws ArithmeticException { ... }
...
}Notice that an immutable rep is particularly easy to argue for safety from rep exposure.
Reading exercises
Consider the following ADT:
// Mutable type representing Twitter users' followers.
public class FollowGraph {
private final Map<String,Set<String>> followersOf;
// Rep invariant:
// all Strings in followersOf are Twitter usernames
// (i.e., nonempty strings of letters, digits, underscores)
// no user follows themselves, i.e. x is not in followersOf.get(x)
// Abstraction function:
// represents the follower graph where Twitter user x is followed by user y
// if and only if followersOf.get(x).contains(y)
// Safety from rep exposure:
// All fields are private, and ???
// Operations (specs and method bodies omitted to save space)
public FollowGraph() { ... }
public void addFollower(String user, String follower) { ... }
public void removeFollower(String user, String follower) { ... }
public Set<String> getFollowers(String user) { ... }
}(missing explanation)
(missing explanation)
(missing explanation)
(missing explanation)
(missing explanation)
(missing explanation)
How to Establish Invariants
An invariant is a property that is true for the entire program – which in the case of an invariant about an object, reduces to the entire lifetime of the object.
To make an invariant hold, we need to:
- make the invariant true in the initial state of the object; and
- ensure that all changes to the object keep the invariant true.
Translating this in terms of the types of ADT operations, this means:
- creators and producers must establish the invariant for new object instances; and
- mutators and observers must preserve the invariant.
The risk of rep exposure makes the situation more complicated. If the rep is exposed, then the object might be changed anywhere in the program, not just in the ADT’s operations, and we can’t guarantee that the invariant still holds after those arbitrary changes. So the full rule for proving invariants is:
Structural induction. If an invariant of an abstract data type is
- established by creators and producers;
- preserved by mutators, and observers; and
- no representation exposure occurs,
then the invariant is true of all instances of the abstract data type.
Reading exercises
Recall this data type from the first exercise in this reading:
/** Represents an immutable right triangle. */
class RightTriangle {
private double[] sides;
// sides[0] and sides[1] are the two legs,
// and sides[2] is the hypotenuse, so declare it to avoid having a
// magic number in the code:
public static final int HYPOTENUSE = 2;
/** Make a right triangle.
* @param legA, legB the two legs of the triangle
* @param hypotenuse the hypotenuse of the triangle.
* Requires hypotenuse^2 = legA^2 + legB^2
* (within the error tolerance of double arithmetic)
*/
public RightTriangle(double legA, double legB, double hypotenuse) {
this.sides = new double[] { legA, legB, hypotenuse };
}
/** Get all the sides of the triangle.
* @return three-element array with the triangle's side lengths
*/
public double[] getAllSides() {
return sides;
}
/** @return length of the triangle's hypotenuse */
public double getHypotenuse() {
return sides[HYPOTENUSE];
}
/** @param factor to multiply the sides by
* @return a triangle made from this triangle by
* multiplies all side lengths by factor.
*/
public RightTriangle scale(double factor) {
return new RightTriangle (sides[0]*factor, sides[1]*factor, sides[2]*factor);
}
/** @return a regular triangle made from this triangle.
* A regular right triangle is one in which
* both legs have the same length.
*/
public RightTriangle regularize() {
double bigLeg = Math.max(side[0], side[1]);
return new RightTriangle (bigLeg, bigLeg, side[2]);
}
}This datatype has an important invariant: the relationship between the legs and hypotenuse, as stated in the Pythagorean theorem.
(missing explanation)
(missing explanation)
(missing explanation)
(missing explanation)
(missing explanation)
ADT invariants replace preconditions
Now let’s bring a lot of pieces together. An enormous advantage of a well-designed abstract data type is that it encapsulates and enforces properties that we would otherwise have to stipulate in a precondition. For example, instead of a spec like this, with an elaborate precondition:
/**
* @param set1 is a sorted set of characters with no repeats
* @param set2 is likewise
* @return characters that appear in one set but not the other,
* in sorted order with no repeats
*/
static String exclusiveOr(String set1, String set2);We can instead use an ADT that captures the desired property:
/** @return characters that appear in one set but not the other */
static SortedSet<Character> exclusiveOr(SortedSet<Character> set1, SortedSet<Character> set2);This is easier to understand, because the name of the ADT conveys all the programmer needs to know. It’s also safer from bugs, because Java static checking comes into play, and the required condition (sorted with no repeats) can be enforced in exactly one place, the SortedSet type.
Many of the places where we used preconditions on the problem sets would have benefited from a custom ADT instead.
Reading exercises
Consider this method:
/**
* Find tweets written by a particular user.
*
* @param tweets a list of tweets with distinct timestamps, not modified by this method.
* @param username Twitter username (a nonempty sequence of letters, digits, and underscore)
* @return all and only the tweets in the list whose author is username,
* in the same order as in the input list.
*/
public static List<Tweet> writtenBy(List<Tweet> tweets, String username) { ... }(missing explanation)
Summary
- An invariant is a property that is always true of an ADT object instance, for the lifetime of the object.
- A good ADT preserves its own invariants. Invariants must be established by creators and producers, and preserved by observers and mutators.
- The rep invariant specifies legal values of the representation, and should be checked at runtime with
checkRep(). - The abstraction function maps a concrete representation to the abstract value it represents.
- Representation exposure threatens both representation independence and invariant preservation.
The topics of today’s reading connect to our three properties of good software as follows:
Safe from bugs. A good ADT preserves its own invariants, so that those invariants are less vulnerable to bugs in the ADT’s clients, and violations of the invariants can be more easily isolated within the implementation of the ADT itself. Stating the rep invariant explicitly, and checking it at runtime with checkRep(), catches misunderstandings and bugs earlier, rather than continuing on with a corrupt data structure.
Easy to understand. Rep invariants and abstraction functions explicate the meaning of a data type’s representation, and how it relates to its abstraction.
Ready for change. Abstract data types separate the abstraction from the concrete representation, which makes it possible to change the representation without having to change client code.