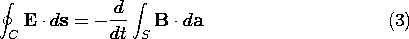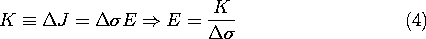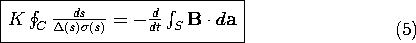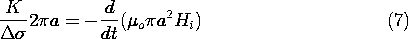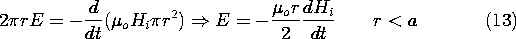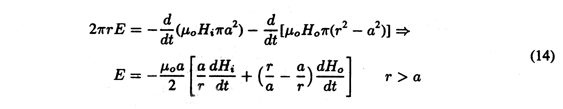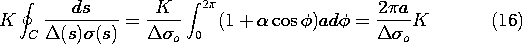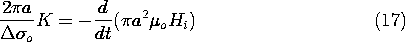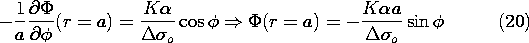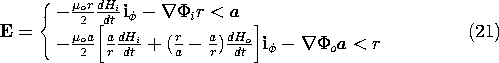10.3
Diffusion of Axial Magnetic FIelds Through ThinConductors

This and the next section are concerned with the influence of thin-sheet conductors of finite conductivity on distributions of magnetic field. The demonstration of the previous section is typical of physical situations of interest. By virtue of Faraday's law, an applied field induces currents in the conducting sheet. Through Ampère's law, these in turn result in an induced field tending to buck out the imposed field. The resulting field has a time dependence reflecting not only that of the applied field but the conductivity and dimensions of the conductor as well. This is the subject of the next two sections.

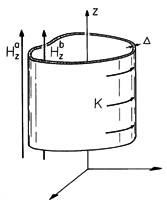
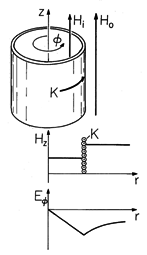
Figure 10.3.1 A thin shell having conductivity and thickness has the shape of a cylinder of arbitrary cross-section. The surface current density K(t) circulates in the shell in a direction perpendicular to the magnetic field, which is parallel to the cylinder axis. A class of configurations with remarkably simple fields involves one or more sheet conductors in the shape of cylinders of infinite length. As illustrated in Fig. 10.3.1, these are uniform in the z direction but have an arbitrary cross-sectional geometry. In this section, the fields are z directed and the currents circulate around the z axis through the thin sheet. Fields and currents are pictured as independent of z.

The current density J is divergence free. If we picture the current density as flowing in planes perpendicular to the z axis, and as essentially uniform over the thickness of the sheet, then the surface current density must be independent of the azimuthal position in the sheet.

Ampère's continuity condition, (9.5.3), requires that the adjacent axial fields are related to this surface current density by

In a system with a single cylinder, with a given circulating surface current density K and insulating materials of uniform properties both outside (a) and inside (b), a uniform axial field inside and no field outside is the exact solution to Ampère's law and the flux continuity condition. (We saw this in Demonstration 8.2.1 and in Example 8.4.2. for a solenoid of circular cross-section.) In a system consisting of nested cylinders, each having an arbitrary cross-sectional geometry and each carrying its own surface current density, the magnetic fields between cylinders would be uniform. Then (2) would relate the uniform fields to either side of any given sheet.

In general, K is not known. To relate it to the axial field, we must introduce the laws of Ohm and Faraday. The fact that K is uniform makes it possible to exploit the integral form of the latter law, applied to a contour C that circulates through the cylinder.

To replace E in this expression, we multiply J = E by the thickness to relate the surface current density to E, the magnitude of E inside the sheet.

If and are uniform, then E (like K), is the same everywhere along the sheet. However, either the thickness or the conductivity could be functions of azimuthal position. If and are given, the integral on the left in (3) can be taken, since K is constant. With s denoting the distance along the contour C, (3) and (4) become

Of most interest is the case where the thickness and conductivity are uniform and (5) becomes

with P denoting the peripheral length of the cylinder.

The following are examples based on this model.

Example 10.3.1. Diffusion of Axial Field into a Circular Tube

The conducting sheet shown in Fig. 10.3.2 has the shape of a long pipe with a wall of uniform thickness and conductivity. There is a uniform magnetic field H = i_z H_o (t) in the space outside the tube, perhaps imposed by means of a coaxial solenoid. What current density circulates in the conductor and what is the axial field intensity H_i inside?

Figure 10.3.2 Circular cylindrical conducting shell with external axial field intensity H_o(t) imposed. The response to a step in applied field is a current density that initially shields the field from the inner region. As this current decays, the field penetrates into the interior and is finally uniform throughout.

Representing Ohm's law and Faraday's law of induction, (6) becomes

Ampère's law, represented by the continuity condition, (2), requires that

In these two expressions, H_o is a given driving field, so they can be combined into a single differential equation for either K or H_i. Choosing the latter, we obtain

where

This expression pertains regardless of the driving field. In particular, suppose that before t = 0, the fields and surface current are zero, and that when t = 0, the outside H_o is suddenly turned on. The appropriate solution to (9) is the combination of the particular solution H_i = H_o and the homogeneous solution exp (-t/_m) that satisfies the initial condition.

It follows from (8) that the associated surface current density is

At a given instant, the axial field has the radial distribution shown in Fig. 10.3.2b. Outside, the field is imposed to be equal to H_o, while inside it is at first zero but then fills in with an exponential dependence on time. After a time that is long compared to _m, the field is uniform throughout. Implied by the discontinuity in field intensity at r = a is a surface current density that initially terminates the outside field. When t = 0, K = -H_o, and this results in a field that bucks out the field imposed on the inside region. The decay of this current, expressed by (12), accounts for the penetration of the field into the interior region.

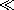
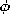
This example illustrates what one means by "perfect conductor approximation." A perfect conductor would shield out the magnetic field forever. A physical conductor shields it out for times t _m. Thus, in the MQS approximation, a conductor can be treated as perfect for times that are short compared with the characteristic time _m. The electric field E E is given by applying (3) to a contour having an arbitrary radius r.

At r = a, this particular solution matches that already found using the same integral law in the conductor. In this simple case, it is not necessary to match boundary conditions by superimposing a homogeneous solution taking the form of a conservative field.

We consider next an example where the electric field is not simply the particular solution.

Example 10.3.2. Diffusion into Tube of Nonuniform Conductivity

Once again, consider the circular cylindrical shell of Fig. 10.3.2 subject to an imposed axial field H_o(t). However, now the conductivity is a function of azimuthal position.

The integral in (5), resulting from Faraday's law, becomes

and hence

Ampère's continuity condition, (2), once again becomes

Thus, H_i is determined by the same expressions as in the previous example, except that is replaced by _o. The surface current response to a step in imposed field is again the exponential of (12).

It is the electric field distribution that is changed. Using (15), (4) gives

for the electric field inside the conductor. The E field in the adjacent free space regions is found using the familiar approach of Sec. 10.1. The particular solution is the same as for the uniformly conducting shell, (13) and (14). To this we add a homogeneous solution E_h = - such that the sum matches the tangential field given by (19) at r = a. The -independent part of (19) is already matched by the particular solution, and so the boundary condition on the homogeneous part requires that

Solutions to Laplace's equation that vary as sin ( ) match this condition. Outside, the appropriate r dependence is 1/r while inside it is r. With the coefficients of these potentials adjusted to match the boundary condition given by (20), it follows that the electric field outside and inside the shell is

where

These expressions can be evaluated using (11) and (12) for H_i and K for the electric field associated with a step in applied field. It follows that E, like the surface current and the induced H, decays exponentially with the time constant of (10). At a given instant, the distribution of E is as illustrated in Fig. 10.3.3. The total solution is the sum of the particular rotational and homogeneous conservative parts. The degree to which the latter influences the total field depends on , which reflects the inhomogeneity in conductivity.

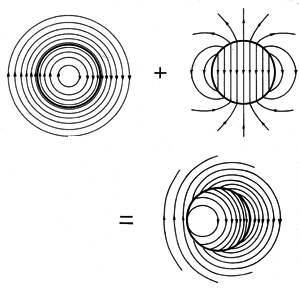
Figure 10.3.3 Electric field induced in regions inside and outside shell (having conductivity that varies with azimuthal position) portrayed as the sum of a particular rotational and homogeneous conservative solution. Conductivity is low on the right and high on the left, = 0.5.

For positive , the conductivity is low on the right (when = 0) and high on the left in Fig. 10.3.3. In accordance with (7.2.8), positive unpaired charge is induced in the transition region where the current flows from high to low conductivity, and negative charge is induced in the transition region from low to high conductivity. The field of the homogeneous solution shown in the figure originates and terminates on the induced charges.

We shall return to models based on conducting cylindrical shells in axial fields. Systems of conducting shells can be used to represent the nonuniform flow of current in thick conductors. The model will also be found useful in determining the rate of induction heating for cylindrical objects.