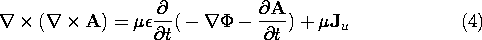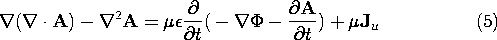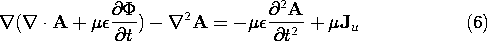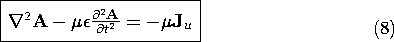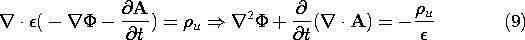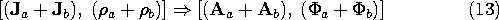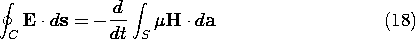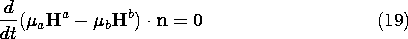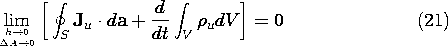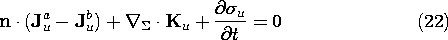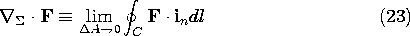12.1
Electrodynamic Fields and Potentials

In this section, we extend the use of the scalar and vector potentials to the description of electrodynamic fields. In regions of interest, the current density J of unpaired charge and the charge density _u are prescribed functions of space and time. If there is any material present, it is of uniform permittivity and permeability , D = E and B = H. For quasistatic fields in such regions, the potentials and A are governed by Poisson's equation. In this section, we see the role of Poisson's equation for quasistatic fields taken over by the inhomogeneous wave equation for electrodynamic fields.

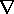
In both Chaps. 4 and 8, potentials were introduced so as to satisfy automatically the one of the two laws that was source free. In Chap. 4, we made E = - so that E was automatically irrotational, x E = 0. In Chap. 8 we let B = x A so that B was automatically solenoidal, B = 0. Of the four laws comprising Maxwell's equations, (12.0.7)-(12.0.10), those of Gauss and Ampère involve sources, while the last two, Faraday's law and the magnetic flux continuity law, do not. Following the approach used before, potentials should be introduced that automatically satisfy Faraday's law and the magnetic flux continuity law, (12.0.9) and (12.0.10). This is the objective of the following steps.

Given that the magnetic flux density remains solenoidal, the vector potential A can be defined just as it was in Chap. 8.

With H represented in this way, (12.0.10) is again automatically satisfied and Faraday's law, (12.0.9), becomes

This expression is also automatically satisfied if we make the quantity in brackets equal to -.

With H and E defined in terms of and A as given by (1) and (3), the last two of the four Maxwell's equations, (12.0.9-12.0.10), are automatically satisfied. Note, however, that the potentials that represent given fields H and E are not fully specified by (1) and (3). We can add to A the gradient of any scalar function, thus changing both A and without affecting H or E. A further specification of the potentials will therefore be given shortly.

We now turn to finding the equations that A and must obey if the laws of Gauss and Ampère, the first two of (12.0.9-12.0.10), are to be satisfied. Substitution of (1) and (3) into Ampère's law, (12.0.8), gives

A vector identity makes it possible to rewrite the left-hand side so that this equation is

With the gradient and time derivative operators interchanged, this expression is

To uniquely specify A, we must not only stipulate its curl, but give its divergence as well. This point was made in Sec. 8.0. In Sec. 8.1, where we were concerned with MQS fields, we found it convenient to make A solenoidal. Here, where we have kept the displacement current, we set the divergence of A so that the term in brackets on the left is zero.

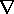
This choice of A is called the choice of the Lorentz gauge. In this gauge, the expression representing Ampère's law, (6), reduces to one involving A alone, to the exclusion of .

The last of Maxwell's equations, Gauss' law, is satisfied by making obey the differential equation that results from the substitution of (3) into (12.0.7).

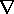
We can substitute for A using (7), thus eliminating A from this expression.

In summary, with H and E defined in terms of the vector potential A and scalar potential by (1) and (3), the distributions of these potentials are governed by the vector and scalar inhomogeneous wave equations (8) and (10), respectively. The unpaired charge density and the unpaired current density are the "sources" in these equations. In representing the fields in terms of the potentials, it is understood that the "gauge" of A has been set so that A and are related by (7).

The time derivatives in (8) and (10) are the result of retaining both the displacement current and the magnetic induction. Thus, in the quasistatic limits, these terms are neglected and we return to vector and scalar potentials governed by Poisson's equation.

Superposition Principle

The inhomogeneous wave equations satisfied by A and [(8) and (10)] as well as the gauge condition, (7), are linear when the sources on the right are prescribed. That is, if solutions A_a and _a are associated with sources J_a and _a,

and similarly, J_b and _b produce the potentials A_b, _b,

then the potentials resulting from the sum of the sources is the sum of the potentials.

The formal proof of this superposition principle follows from the same reasoning used for Poisson's equation in Sec. 4.3.

In prescribing the charge and current density on the right in (8) and (10), it should be remembered that these sources are related by the law of charge conservation. Thus, although and A appear in (8) and (10) to be independent, they are actually coupled. This interdependence of the sources is reflected in the link between the scalar and vector potentials established by the gauge condition of (7). Once A has been found, it is often convenient to use this relation to determine .

Continuity Conditions

Each of Maxwell's equations, (12.0.7)-(12.0.10), as well as the charge conservation law obtained by combining the divergence of Ampère's laws with Gauss' law, implies a continuity condition. In the absence of polarization and magnetization, these conditions were derived from the integral laws in Chap. 1. Generalized to include polarization and magnetization in Chaps. 6 and 9, the continuity conditions for (12.0.7)-(12.0.10) are, respectively,

The derivation of these conditions is the same as given at the end of the sections introducing the respective integral laws in Chap. 1, except that _o H is replaced by H in Faraday's law and _o E by E in Ampère's law.

In Secs. 12.6 and 12.7, and in the following chapters, these conditions are used to relate electrodynamic fields to surface currents and surface charges. At the outset, we recognize that two of these continuity conditions are, like Faraday's law and the law of magnetic flux continuity, not independent of each other. Further, just as the laws of Ampère and Gauss imply the charge conservation relation between J_u and _u, the continuity conditions associated with these laws imply the charge conservation continuity condition obeyed by the surface currents and surface charge densities.

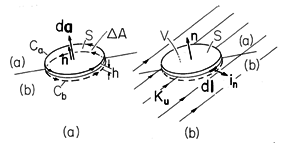
To see the first interdependence, Faraday's law is integrated over a surface S enclosed by a contour C lying in the plane of the interface, as shown in Fig. 12.1.1a. Stokes' theorem is then used to write

Figure 12.1.1 (a) Surface S just above or just below the interface. (b) Volume V of incremental thickness h enclosing a section of the interface.

Whether taken on side (a) or side (b) of the interface, the line integral on the left is the same. This follows from Faraday's continuity law (16). Thus, if we take the difference between (18) evaluated on side (a) and on side (b), we obtain

By making the tangential electric field continuous, we have assured the continuity of the time derivative of the normal magnetic flux density. For a sinusoidally time-dependent process, matching the tangential electric field automatically assures the matching of the normal magnetic flux densities.

In particular, consider a surface of a conductor that is "perfect" in the MQS sense. The electric field inside such a conductor is zero. From (16), the tangential component of E just outside the conductor must also be zero. In view of (19), we conclude that the normal flux density at a perfectly conducting surface must be time independent. This boundary condition is familiar from the last half of Chap. 8.

---

²Note that the absence of a time-varying normal flux density does not imply that there is no tangential E. The surface of a material that is an infinite conductor in one direction but an insulator in the other might have no normal H and yet support a tangential E in the direction of zero conductivity.

---

Given that the divergence of Ampère's law combines with Gauss' law to give conservation of charge,

we should expect that there is a second relationship among the conditions of (14)-(17), this time between the surface charge density and surface current density that appear in the first two. Integration of (20) over the volume of the "pillbox" shown in Fig. 12.1.1b gives

In the limit where first the thickness h and then the area A go to zero, these integrals reduce to A times

The first term is the contribution to the first integral in (21) from the surfaces on the (a) and (b) sides of the interface, respectively, having normals +n and -n. The second term, which is written in terms of the "surface divergence" defined in terms of a vector F by

results because the surface current density makes a finite contribution to the first integral in (21) even though the thickness h of the volume goes to zero. [In (23), i_n is the unit normal to the volume V, as shown in the figure.] Such a surface current density can be used to represent currents imposed over a region having a thickness that is small compared to other dimensions of interest. It can also represent the current on the surface of a perfect conductor. (In using the conservation of charge continuity condition in Secs. 7.6 and 7.7, this term was not present because the surfaces described by this continuity condition were not carrying surface currents.) In terms of coordinates local to the point of interest, the surface divergence can be thought of as a two-dimensional divergence. The last term in (22) results from the integration of the charge density over the volume. Because there is a surface charge density, there is net charge inside the volume even in the limit where h 0.

When we specify K_u and _u in (14) and (15), it is with the understanding that they obey the charge conservation continuity condition, (22). But, we also conclude that the charge conservation law is implied by the laws of Ampère and Gauss, and so we know that if (14) and (15) are satisfied, then so too is (22).

When perfectly conducting boundaries are described in Chaps. 13 and 14, the surface current and charge found on a perfectly conducting boundary using the continuity conditions from the laws of Ampère and Gauss will automatically satisfy the charge conservation condition. Further, a zero tangential electric field on a perfect conductor automatically implies that the normal magnetic flux density vanishes.

With the inhomogeneous wave equation playing the role of Poisson's equation, the stage is now set for a scenario paralleling that for electroquasistatics in Chap. 4 and for magnetoquasistatics in Chap. 8. The next section identifies the fields associated with source singularities. Section 12.3 develops superposition integrals for the response to given distributions of the sources. Henceforth, in this and the next chapter, we shall drop the subscript u from the source quantities.