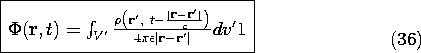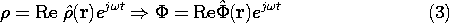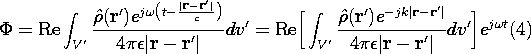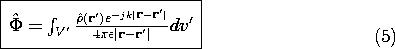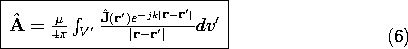12.3
Superposition Integral for Electrodynamic Fields

With the identification in Sec. 12.2 of the fields associated with point charge and current sources, we are ready to construct fields produced by an arbitrary distribution of sources. Just as the superposition integral of Sec. 4.5 was based on the linearity of Poisson's equation, the superposition principle for the dynamic fields hinges on the linear nature of the inhomogeneous wave equations of Sec. 12.1.

Transient Response

The scalar potential for a point charge q at the origin, given by (12.2.1), can be generalized to describe a point charge at an arbitrary source position r^' by replacing the distance r by |r - r^'| (see Fig. 4.5.1). Then, the point charge is replaced by the charge density evaluated at the source position multiplied by the incremental volume element dv^'. With these substitutions in the scalar potential of a point charge, (12.2.1), the potential at an observer location r is the integrand of the expression

The integration over the source coordinates r^' then superimposes the fields at r due to all of the sources. Given the charge density everywhere, this integral comprises the solution to the inhomogeneous wave equation for the scalar potential, (12.1.10).

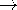
In Cartesian coordinates, any one of the components of the vector inhomogeneous wave-equation, (12.1.8), obeys a scalar equation. Thus, with / J_i, (1) becomes the solution for A_i, whether i be x, y or z.

We should keep in mind that conservation of charge implies a relationship between the current and charge densities of (1) and (2). Given the current density, the charge density is determined to within a time-independent distribution. An alternative, and often less involved, approach to finding E avoids the computation of the charge density. Given J , A is found from (2). Then, the gauge condition, (12.1.7), is used to find . Finally, E is found from (12.1.3).

Sinusoidal Steady State Response

In many practical situations involving radio, microwave, and optical frequency systems, the sources are essentially in the sinusoidal steady state.

Equation (1) is evaluated by using the charge density given by (3), with r r^' and t t - |r - r^'|/c

where k /c. Thus, the quantity in brackets in the second expression is the complex amplitude of at the location r. With the understanding that the time dependence will be recovered by multiplying this complex amplitude by exp (j t) and taking the real part, the superposition integral for the complex amplitude of the potential is

From (2), the same reasoning gives the superposition integral for the complex amplitude of the vector potential.

The superposition integrals are often used to find the radiation patterns of driven antenna arrays. In these cases, the distribution of current, and hence charge, is independently prescribed everywhere. Section 12.4 illustrates this application of the superposition integral.

If fields are to be found in confined regions of space, with part of the source distribution on boundaries, the fields given by the superposition integrals represent particular solutions to the inhomogeneous wave equations. Following the same approach as used in Sec. 5.1 for solving boundary value problems involving Poisson's equation, the boundary conditions can then be satisfied by superimposing on the solution to the inhomogeneous wave equation solutions satisfying the homogeneous wave equation.