Aerodynamic Networks

Aerodynamic networks are made of a concatenation of network elements filled with a compressible medium which can be considered as an ideal gas. An ideal gas satisfies

$$p=\rho R \theta,$$ (130)

where p is the pressure, $\rho$ is the density, $R$ is the specific gas constant and $\theta$ is the absolute temperature. A network element (see section 6.2.28) consists of three nodes: in the corner nodes the temperature and pressure are the unknowns, in the midside node the mass flow is unknown. The corner nodes play the role of crossing points in the network, whereas the midside nodes represent the flow within one element. To determine these unknowns, three types of equations are available: conservation of mass and conservation of energy in the corner nodes and conservation of momentum in the midside node. Right now, only stationary flow is considered.

The stationary form of the conservation of mass for compressible fluids is expressed by:

$$\mathbf{\nabla} \cdot ( \rho \mathbf{v}) = 0$$ (131)

where $\mathbf{v}$ the velocity vector. Integration over all elements connected to corner node i yields:

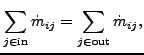$$\sum_{j \in \text{in}} \dot{m}_{ij} = \sum_{j \in \text{out}} \dot{m}_{ij},$$ (132)

where $\dot{m}_{ij}$ is the mass flow from node i to node j or vice versa. In the above equation $\dot{m}_{ij}$ is always positive.

The conservation of momentum or element equations are specific for each type of fluid section attributed to the element and are discussed in Section 6.3 on fluid sections. For an element with corner nodes i,j it is generally of the form $f({p_{tot}}_i, {\theta_{tot}}_i, \dot{m}_{ij},{p_{tot}}_j)=0$ (for positive $\dot{m}_{ij}$, where p is the total pressure and $\theta_{tot}$ is the total temperature), although more complex relationships exist. Notice in particular that the temperature pops up in this equation (this is not the case for hydraulic networks).

The conservation of energy in stationary form requires ([23]):

$$\mathbf{\nabla} \cdot (\rho h_{tot} \mathbf{v}) = - \mathbf{\nabla} \cdot \mathbf{q} + \rho h^{\theta} + \rho \mathbf{f} \cdot \mathbf{v},$$ (133)

where $\mathbf{q}$ is the external heat flux, $h^{\theta}$ is the body flux per unit of mass and $\mathbf{f}$ is the body force per unit of mass. $h_{tot}$ is the total enthalpy satisfying:

$$h_{tot} = c_p \theta + \frac{\mathbf{v} \cdot \mathbf{v}}{2},$$ (134)

where $c_p$ is the specific heat at constant pressure and $\theta$ is the absolute temperature (in Kelvin). This latter formula only applies if $c_p$ is considered to be independent of the temperature. This is largely true for a lot of industrial applications. In this connection the reader be reminded of the definition of total temperature and total pressure (also called stagnation temperature and stagnation pressure, respectively):

$$\theta_{tot} = \theta + \frac{\mathbf{v} \cdot \mathbf{v}}{2 c_p},$$ (135)

and

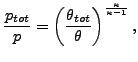$$\frac{p_{tot}}{p} = \left( \frac{\theta_{tot}}{\theta} \right) ^ {\frac{\kappa}{\kappa-1}},$$ (136)

where $\kappa = c_p/c_v$. $\theta$ and $p$ are also called the static temperature and static pressure, respectively.

If the corner nodes of the elements are considered to be large chambers, the velocity $\mathbf{v}$ is zero. In that case, the total quantities reduce to the static ones, and integration of the energy equation over all elements belonging to end node $i$ yields [17]:

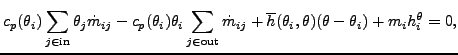$$c_p (\theta_i) \sum_{j \in \text{in}} \theta_j \dot{m}_{ij} - c_p... ...{ij} + \overline{h}(\theta_i, \theta) (\theta - \theta_i) + m_i h_i^{\theta}=0,$$ (137)

where $\overline{h}(\theta_i,\theta)$ is the convection coefficient with the walls. Notice that, although this is not really correct, a slight temperature dependence of $c_p$ is provided for. If one assumes that all flow entering a node must also leave it and taking for both the $c_p$ value corresponding to the mean temperature value of the entering flow, one arrives at:

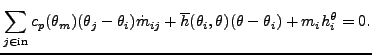$$\sum_{j \in \text{in}} c_p (\theta_m) (\theta_j-\theta_i) \dot{m}_{ij} + \overline{h}(\theta_i, \theta) (\theta - \theta_i) + m_i h_i^{\theta}=0.$$ (138)

where $\theta_m=(\theta_i+\theta_j)/2$.

The calculation of aerodynamic networks is triggered by the *HEAT TRANSFER keyword card. Indeed, such a network frequently produces convective boundary conditions for solid mechanics heat transfer calculations. However, network calculations can also be performed on their own.

A particularly delicate issue in networks is the number of boundary conditions which is necessary to get a unique solution. To avoid ending up with more or less equations than unknowns, the following rules should be obeyed:

• The pressure and temperature should be known in those nodes where mass flow is entering the network. Since it is not always clear whether at a specific location mass flow is entering or leaving, it is advisable (though not necessary) to prescribe the pressure and temperature at all external connections, i.e in the nodes connected to dummy network elements.
• A node where the pressure is prescribed should be connected to a dummy network element. For instance, if you have a closed circuit add an extra dummy network element to the node in which you prescribe the pressure.

Output variables are the mass flow (key MF on the *NODE PRINT or *NODE FILE card), the total pressure (key PN -- network pressure -- on the *NODE PRINT card and PT on the *NODE FILE card) and the total temperature (key NT on the *NODE PRINT card and TT on the *NODE FILE card). Notice that the labels for the *NODE PRINT keyword are more generic in nature, for the *NODE FILE keyword they are more specific. These are the primary variables in the network. In addition, the user can also request the static temperature (key TS on the *NODE FILE card). Internally, in network nodes, components one to three of the structural displacement field are used for the mass flow, the total pressure and the static temperature, respectively. So their output can also be obtained by requesting U on the *NODE PRINT card.