Subsections
18.5 Heat Exchangers
The general function of a heat exchanger is to transfer heat from
one fluid to another. The basic component of a heat exchanger can be
viewed as a tube with one fluid running through it and another fluid
flowing by on the outside. There are thus three heat transfer
operations that need to be described:
- Convective heat transfer
from fluid to the inner wall of the tube,
- Conductive heat
transfer through the tube wall, and
- Convective heat transfer from the
outer tube wall to the outside fluid.
Heat exchangers are typically classified according to flow
arrangement and type of construction. The simplest heat exchanger is
one for which the hot and cold fluids move in the same or opposite
directions in a concentric tube (or double-pipe) construction. In
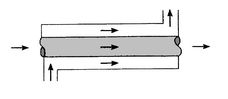
the parallel-flow arrangement of
Figure 18.8(a), the hot and cold fluids
enter at the same end, flow in the same direction, and leave at the
same end. In the counterflow arrangement of
Figure 18.8(b), the fluids enter at
opposite ends, flow in opposite directions, and leave at opposite
ends.
Figure 18.8:
Concentric tubes heat exchangers
[Parallel flow]
[Counterflow]
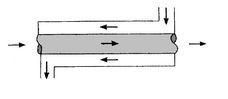
|
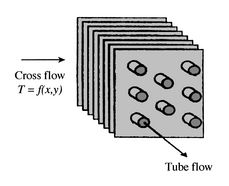
Figure 18.9:
Cross-flow heat
exchangers.
[Finned with both
fluids unmixed.]
[Unfinned
with one fluid mixed and the other unmixed]
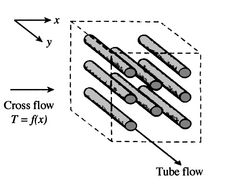
|
Alternatively, the fluids may be in cross flow (perpendicular to
each other), as shown by the finned and unfinned tubular heat
exchangers of Figure 18.9. The two
configurations differ according to whether the fluid moving over the
tubes is unmixed or mixed. In
Figure 18.9(a), the fluid is said to be
unmixed because the fins prevent motion in a direction (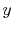 ) that is
transverse to the main flow direction (
) that is
transverse to the main flow direction (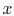 ). In this case the fluid
temperature varies with
). In this case the fluid
temperature varies with 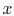 and
and 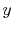 . In contrast, for the unfinned
tube bundle of Figure 18.9(b), fluid
motion, hence mixing, in the transverse direction is possible, and
temperature variations are primarily in the main flow direction.
Since the tube flow is unmixed, both fluids are unmixed in the
finned exchanger, while one fluid is mixed and the other unmixed in
the unfinned exchanger.
. In contrast, for the unfinned
tube bundle of Figure 18.9(b), fluid
motion, hence mixing, in the transverse direction is possible, and
temperature variations are primarily in the main flow direction.
Since the tube flow is unmixed, both fluids are unmixed in the
finned exchanger, while one fluid is mixed and the other unmixed in
the unfinned exchanger.
To develop the methodology for heat exchanger analysis and design,
we look at the problem of heat transfer from a fluid inside a tube
to another fluid outside.
Figure 18.10:
Geometry for heat
transfer between two fluids
|
|
We examined this problem before in
Section 17.2 and found that the heat
transfer rate per unit length is given by
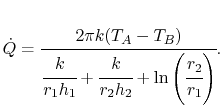 |
(18..21) |
Here we have taken into account one additional thermal resistance
than in Section 17.2, the resistance
due to convection on the interior, and include in our expression for
heat transfer the bulk temperature of the fluid, 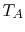 , rather than
the interior wall temperature,
, rather than
the interior wall temperature, 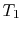 .
.
It is useful to define an overall heat transfer coefficient 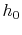 per unit length as
per unit length as
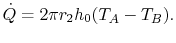 |
(18..22) |
From (18.21) and (18.22)
the overall heat transfer coefficient, 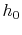 , is
, is
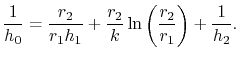 |
(18..23) |
We will make use of this in what follows.
Figure 18.11:
Counterflow heat exchanger
|
|
A schematic of a counterflow heat exchanger is shown in
Figure 18.11. We wish to know the
temperature distribution along the tube and the amount of heat
transferred.
18.5.1 Simplified Counterflow Heat Exchanger (With Uniform Wall Temperature)
To address this we start by considering the general case of axial
variation of temperature in a tube with wall at uniform temperature
 and a fluid flowing inside the tube
(Figure 18.12).
and a fluid flowing inside the tube
(Figure 18.12).
Figure 18.12:
Fluid temperature
distribution along the tube with uniform wall temperature
|
|
The objective is to find the mean temperature of the fluid at 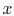 ,
,
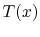 , in the case where fluid comes in at
, in the case where fluid comes in at 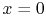 with temperature
with temperature
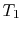 and leaves at
and leaves at 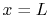 with temperature
with temperature 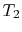 . The expected
distribution for heating and cooling are sketched in
Figure 18.12.
. The expected
distribution for heating and cooling are sketched in
Figure 18.12.
For heating (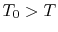 ), the heat flow from the pipe wall in a
length
), the heat flow from the pipe wall in a
length 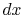 is
is
where 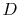 is the pipe diameter. The heat given to the fluid (the
change in enthalpy) is given by
is the pipe diameter. The heat given to the fluid (the
change in enthalpy) is given by
where 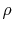 is the density of the fluid,
is the density of the fluid, 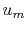 is the mean velocity
of the fluid,
is the mean velocity
of the fluid, 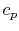 is the specific heat of the fluid and
is the specific heat of the fluid and 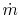 is the mass flow rate of the fluid. Setting the last two expressions
equal and integrating from the start of the pipe, we find
is the mass flow rate of the fluid. Setting the last two expressions
equal and integrating from the start of the pipe, we find
Carrying out the integration,
i.e.,
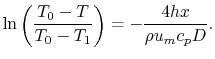 |
(18..24) |
Equation (18.24) can be written as
where
This is the temperature distribution along the pipe. The exit
temperature at 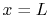 is
is
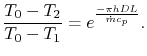 |
(18..25) |
The total heat transfer to the wall all along the pipe is
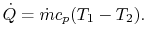 |
(18..26) |
From Equation (18.25),
The total rate of heat transfer is therefore
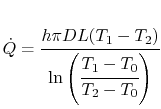 |
|
or
|
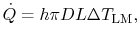 |
(18..27) |
where
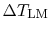 is the logarithmic mean
temperature difference, defined as
is the logarithmic mean
temperature difference, defined as
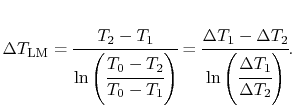 |
(18..28) |
The concept of a logarithmic mean temperature difference is useful
in the analysis of heat exchangers. We will define a logarithmic
mean temperature difference for the general counterflow heat
exchanger below.
We return to our original problem, to
Figure 18.11, and write an
overall heat balance between the two counterflowing streams as
From a local heat balance, the heat given up by stream 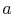 in length
in length
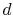 x is
x is
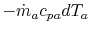 . (There is a negative sign since
. (There is a negative sign since
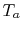 decreases). The heat taken up by stream
decreases). The heat taken up by stream 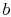 is
is
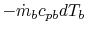 . (There is a negative sign because
. (There is a negative sign because 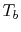 decreases as
decreases as
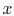 increases). The local heat balance is
increases). The local heat balance is
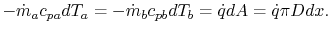 |
(18..29) |
Solving (18.29) for 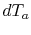 and
and 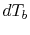 ,
we find
,
we find
where
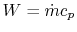 . Also,
. Also,
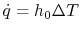 where
where 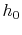 is the overall heat transfer coefficient. We can then say
is the overall heat transfer coefficient. We can then say
Integrating from 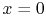 to
to 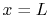 gives
gives
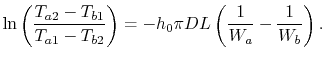 |
(18..30) |
Equation (18.30) can also be written
as
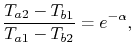 |
(18..31) |
where
We know that
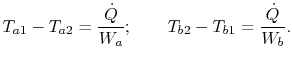 |
(18..32) |
Thus
Solving for the total heat transfer:
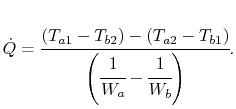 |
(18..33) |
Rearranging (18.30) allows us to
express
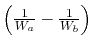 in terms of other
parameters as
in terms of other
parameters as
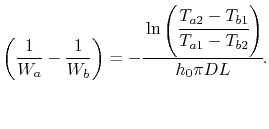 |
(18..34) |
Substituting (18.34) into
(18.33) we obtain a final expression
for the total heat transfer for a counterflow heat exchanger:
This is the generalization (for non-uniform wall temperature) of our
result from Section 18.5.1.
18.5.3 Efficiency of a Counterflow Heat Exchanger
Suppose we know only the two
inlet temperatures 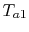 ,
, 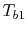 , and we need to find the
outlet temperatures. From (18.31),
, and we need to find the
outlet temperatures. From (18.31),
Eliminating 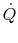 from (18.32),
from (18.32),
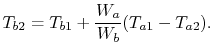 |
(18..38) |
We now have two equations, (18.37) and
(18.38), and two unknowns, 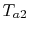 and
and 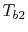 .
Solving first for
.
Solving first for 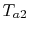 ,
,
or
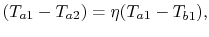 |
(18..39) |
where 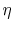 is the efficiency of a counterflow heat exchanger:
is the efficiency of a counterflow heat exchanger:
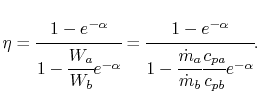 |
(18..40) |
Equation 18.39 gives 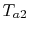 in
terms of known quantities. We can use this result in
(18.38) to find
in
terms of known quantities. We can use this result in
(18.38) to find 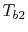 :
:
We examine three examples.
-
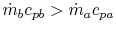
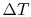 can approach zero at cold end.
can approach zero at cold end.
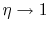 as
as 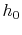 , surface area,
, surface area,
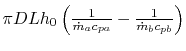 .
.
Maximum value of ratio
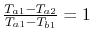
Maximum value of ratio
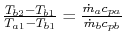 .
.
-
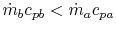
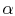 is negative,
is negative,
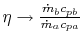 as
as
![$ [\;]\rightarrow\infty\;(W_b < W_a)$](img2222.png)
Maximum value of ratio
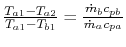
Maximum value of ratio
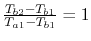 .
.
-
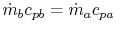
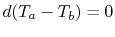
temperature difference remains uniform, 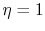 .
.
UnifiedTP
|


 [Unfinned
with one fluid mixed and the other unmixed]
[Unfinned
with one fluid mixed and the other unmixed]

![]() ) that is
transverse to the main flow direction (
) that is
transverse to the main flow direction (![]() ). In this case the fluid
temperature varies with
). In this case the fluid
temperature varies with ![]() and
and ![]() . In contrast, for the unfinned
tube bundle of Figure 18.9(b), fluid
motion, hence mixing, in the transverse direction is possible, and
temperature variations are primarily in the main flow direction.
Since the tube flow is unmixed, both fluids are unmixed in the
finned exchanger, while one fluid is mixed and the other unmixed in
the unfinned exchanger.
. In contrast, for the unfinned
tube bundle of Figure 18.9(b), fluid
motion, hence mixing, in the transverse direction is possible, and
temperature variations are primarily in the main flow direction.
Since the tube flow is unmixed, both fluids are unmixed in the
finned exchanger, while one fluid is mixed and the other unmixed in
the unfinned exchanger.
![]() per unit length as
per unit length as
![]() ,
,
![]() , in the case where fluid comes in at
, in the case where fluid comes in at ![]() with temperature
with temperature
![]() and leaves at
and leaves at ![]() with temperature
with temperature ![]() . The expected
distribution for heating and cooling are sketched in
Figure 18.12.
. The expected
distribution for heating and cooling are sketched in
Figure 18.12.
![]() ), the heat flow from the pipe wall in a
length
), the heat flow from the pipe wall in a
length ![]() is
is
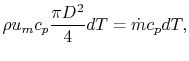
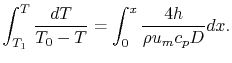
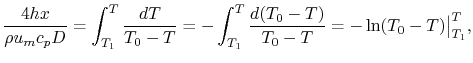
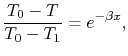
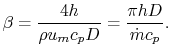
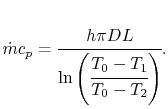
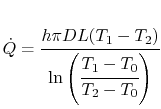
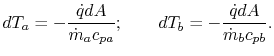
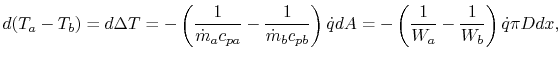
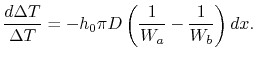
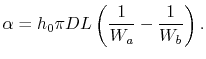
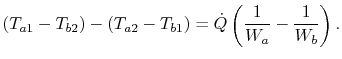
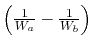 in terms of other
parameters as
in terms of other
parameters as
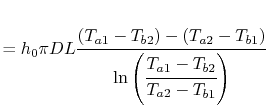
![]() ,
, ![]() , and we need to find the
outlet temperatures. From (18.31),
, and we need to find the
outlet temperatures. From (18.31),
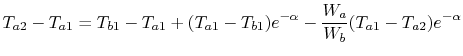
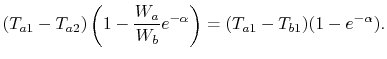
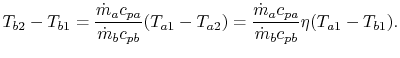
![]() can approach zero at cold end.
can approach zero at cold end.
![]() as
as ![]() , surface area,
, surface area,
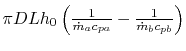 .
.
![]()
![]() .
.
![]() is negative,
is negative,
![]() as
as
![]()
![]()
![]() .
.
![]()
![]() .
.