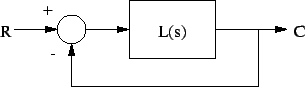
The Barkhausen Stability Criterion is simple, intuitive, and
wrong. During the study of the phase margin of linear systems, this
criterion is often suggested by students grasping for an intuitive
understanding of stability. Unfortunately, although counterexamples are
easy to provide, I do not know of a satisfying disproof to the
Barkhausen Stability Criterion that combats this intuition.
Some textbooks even state the Barkhausen Stability Criterion (although
none refer to it by name). In their introduction of the Nyquist
Stability Criterion, Chestnut and Meyer state
If in a closed-loop control system with sinusoidal excitation the
feedback signal from the controlled variable is in phase and is equal or
greater in magnitude to the reference input at any one frequency, the
system is unstable.[3, page 142]
They continue to insist that ``[t]he Nyquist stability criterion
presents this fact in a rigorous mathematical form.'' This introduction
is completely wrong, and Chestnut and Mayer even provide the Nyquist plot
of a perfect counterexample a mere fourteen pages later (while defining
conditionally-stable nonlinear systems).
The history of the Barkhausen Stability Criterion is an unfortunate one.
In 1921, during his study of feedback oscillators, Barkhausen developed
a ``formula for self-excitation''
where K is an amplifier gain factor and
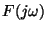 is the frequency
dependence of the feedback loop. This equation was originally intended
for the determination of the oscillation frequency for use in radio
transmitters. However, before conditionally-stable nonlinear systems
were understood, it was widely believed that only a single value of K
separated stable and unstable regions of behavior. Thus, Barkhausen's
Criterion was incorrectly used as a stability criterion, especially in
the German literature [6].
is the frequency
dependence of the feedback loop. This equation was originally intended
for the determination of the oscillation frequency for use in radio
transmitters. However, before conditionally-stable nonlinear systems
were understood, it was widely believed that only a single value of K
separated stable and unstable regions of behavior. Thus, Barkhausen's
Criterion was incorrectly used as a stability criterion, especially in
the German literature [6].
The concept, as stated by Chestnut and Mayer, seems intellectually
satisfying. In fact, I've often had students (and professors) ask,
``But if the gain around the loop is five, and the total phase shift
around the loop is exactly zero, then doesn't that imply that any signal
around the loop will grow with time?''
This reasoning, although deeply flawed, seems to make sense. There is
no shortage of counterexamples, such as
Yet quoting a counterexample rarely satisfies the student. Dislodging
this intuitive misconception is an uphill battle. Thus, it is worth
refuting this argument in every possible way.
Using Black's Formula provides one refutation. For a system with unity
negative feedback and loop transfer function L(s), the closed-loop
transfer function is
Clearly, if we know that
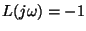 at some frequency, then we know
that the system is unstable. However, knowing that the loop transfer
function is negative and larger than one at one particular frequency
gives us no information about stability. For example, if all we know is
that
at some frequency, then we know
that the system is unstable. However, knowing that the loop transfer
function is negative and larger than one at one particular frequency
gives us no information about stability. For example, if all we know is
that
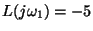 ,
then perhaps L(s)=-5 for all s. Thus
,
then perhaps L(s)=-5 for all s. Thus
Knowing the magnitude and phase at one frequency does not give us enough
information to assess stability.
In a root-locus sense, knowing that
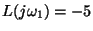 only means that
for less loop gain, we would have closed-loop poles on the imaginary
axis. However, we do not know if increasing the gain fivefold moved the
closed-loop poles into the left half-plane or into the right half-plane.
only means that
for less loop gain, we would have closed-loop poles on the imaginary
axis. However, we do not know if increasing the gain fivefold moved the
closed-loop poles into the left half-plane or into the right half-plane.
In a Nyquist sense, knowing that
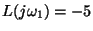 only means that there
may be encirclements of the s=-1 point. However, this fact alone is
not enough information to assess stability. Without more information,
we cannot tell how many encirclements there are (or what direction the
encirclements are in) or even how many open-loop poles are in the right
half-plane. We do not have enough information to determine the number
of closed-loop poles in the right half-plane (Z=N+P), because we know
neither the number of encirclements N, nor the number of open-loop
poles in the right half-plane, P.
only means that there
may be encirclements of the s=-1 point. However, this fact alone is
not enough information to assess stability. Without more information,
we cannot tell how many encirclements there are (or what direction the
encirclements are in) or even how many open-loop poles are in the right
half-plane. We do not have enough information to determine the number
of closed-loop poles in the right half-plane (Z=N+P), because we know
neither the number of encirclements N, nor the number of open-loop
poles in the right half-plane, P.
Unless we know that
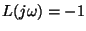 for some frequency, knowing the
value of the loop transfer function at one frequency gives us no
information about stability. Down with Barkhausen!
for some frequency, knowing the
value of the loop transfer function at one frequency gives us no
information about stability. Down with Barkhausen!
Kent H Lundberg
2002-11-14