In holography, coherence properties of sources are very important. In experiment, we often need to know the degree of coherence of any two points at some distance from an incoherent source. We derived the behavior of coherence function for generalized incoherent sources, two-dimensional (2D, like a spinning disk) and 3D (volume incoherent sources). We obtained the coherence patterns originating from incoherent volume sources. Further, we found that the maximum coherence is obtained along radial lines diverging away from the source center, branching out at certain locations. The dependence of the decay of coherence as function of source thickness was also characterized.

Consider the geometry in Fig.1. We are interested in the degree of coherence between point P(r1) at reference plane Π1 located a distance z1 from the coordinate origin and point Q(r2) located at a different plane Π2 with distance Δz to Π1.

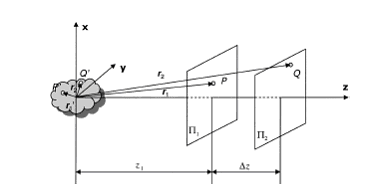
Fig. 1. Illustration of coherence that originates from a quasi-monochromatic, spatially incoherent volume source

For a disk source, with one reference point P(r1) fixed as in Fig. 2, we can calculate the coherence distribution as a function of Q(r2). The exact contour of the coherence in the cross section at plane S (Fig. 2) is indentical to Fig.8.41 of Ref. 1. The locus of maximum coherence is shown in Fig.2.

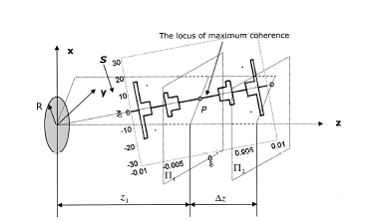
Fig. 2. Illustration of coherence that originates from a quasi-monochromatic, spatially incoherent disk source

The complex degree of coherence from the cylindrical quasi-monochromatic, spatially incoherent source is the coherent superposition of many disk sources stacked in the z direction although every point is totally incoherent inside the volume. The coherence pattern is shown in Fig. 3(b), and the locus of maximum coherence is shown in Fig 3(a).

(a)

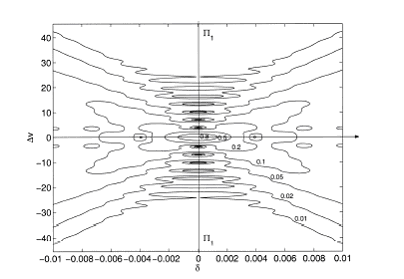
(b)
Fig. 3. (a) Illustration of coherence that originates from a quasi-monochromatic, spatially incoherent cylindrical source (b) contour map of the coherence that originates from a cylindrical source in the cross section at plane S (Fig 3. (a)).

The effect of thickness of the cylinder on the degree of maximum coherence is minimal, as shown in Fig. 4. We should not expect to get much more incoherence through increase the thickness of the incoherent source.

Fig. 4. Modulus of the degree of maximum coherence from 3 cylindrical source with different thickness.

Based on these, we are performing the experiments to verify our derivation and simulation. More properties of arbitrary shapes of volume incoherent sources and surface incoherent sources are also being explored. Because volume incoherent source originates a certain coherence pattern, from it we can track back the shape information of volume incoherent sources. In general, the object we want to image can be seen as a volume incoherent source or surface incoherent source. Then this idea gives us a possible imaging scheme.

Please refer our paper [2] for more details.

[1]. M. Born and E. Wolf, Principles of Optics, 6th ed. (Pergamon, London, 1980).
[2]. K.Tian and G. Barbastathis. “Coherence patterns originating from incoherent volume sources,” Opt. Lett. 29(7), 670-672(2004)

BACK TO TOP