Solvers are presented with a series of geometrical pictures, arrayed in mathematical equations. Each picture starts with the base image of a triangle, and somehow constructs a point inside the triangle, which is marked with an “X.”
The use of the letter X in the title and on the points suggests the Encyclopedia of Triangle Centers, which uses X(n) to assign a canonical ordering to triangle centers. For example, X(1) is the incenter, X(2) is the centroid, etc.
Here is the full set of triangles used in the puzzle (we call the triangle ABC throughout, despite it not being labeled in the puzzle):
| Picture | Center | Explanation |
|---|---|---|
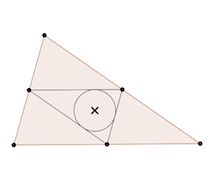 |
X(10) | Shown in the diagram is the incenter of the triangle determined by the midpoints of the sides. The Spieker Center, X(10), is by definition the incenter of the medial triangle |
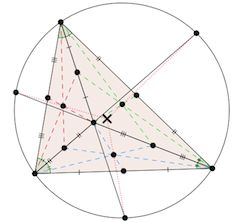 |
X(21) | There’s a lot going on in this picture, so let’s break it down. Constructed first is the incenter I, the intersection of the angle bisectors. The dotted lines give all three medians in triangles AIB, BIC, CIA, which concur at the respective centroids. The other important piece of information is the geometric fact that the circumcenter of the triangle BIC is exactly the intersection of AI with the circumcircle of ABC (this can be proven using angles). Then, the lines that concur at X are the Euler lines of triangles AIB, AIC, BIC, which meet at the Schiffler point X(21) |
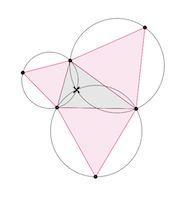 |
X(13) | X(13) is the Fermat point, or Fermat-Torricelli point. From the construction shown, it follows that ∠AXB=∠AXC=∠BXC=120. X(13) is the unique point with this property (for an acute triangle). |
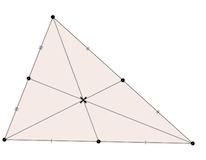 |
X(2) | The centroid X(2) is the intersection of the lines joining each vertex with the midpoint of the opposite side. |
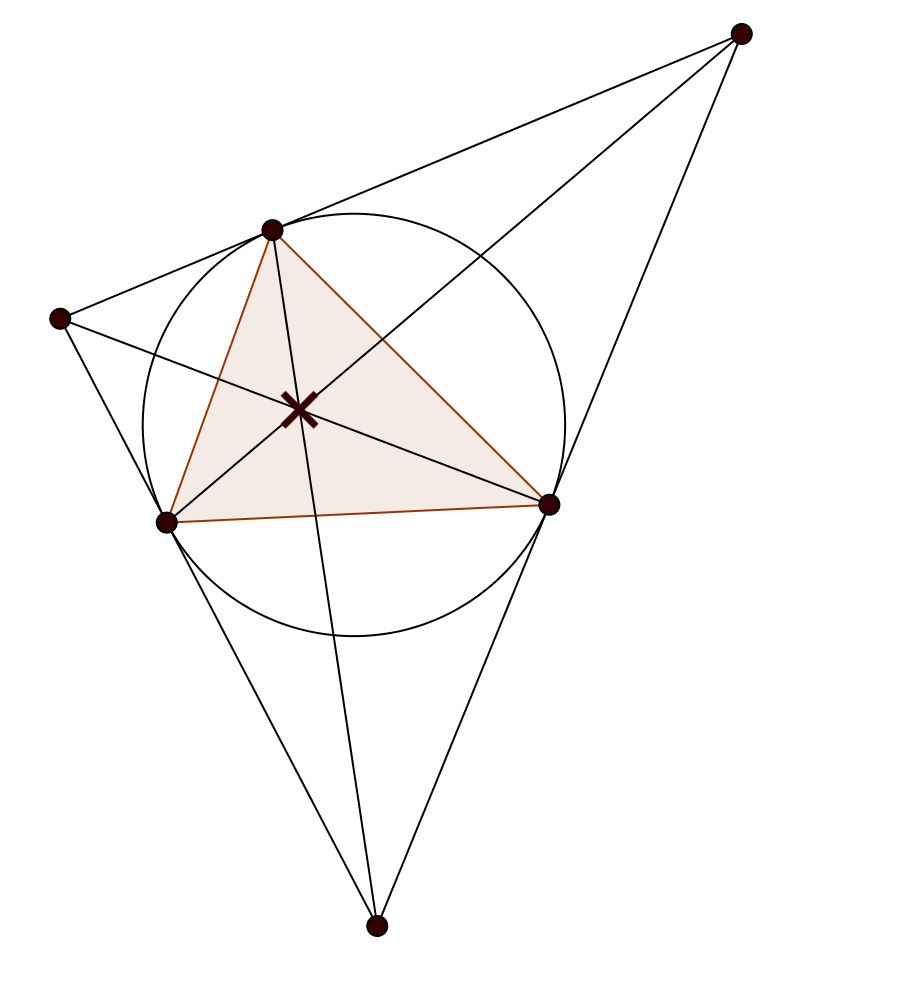 |
X(6) | The symmedian point X(6) is the perspector of ABC and its tangential triangle. The tangential triangle is formed by the tangents to the circumcircle at the three points, and the perspector of two triangles is the intersection of lines through the corresponding vertices, if they concur. This fact is a somewhat deep geometric theorem that is not found on ETC, but does show up on the Wolfram Mathworld pages for both the tangential triangle and symmedian point. |
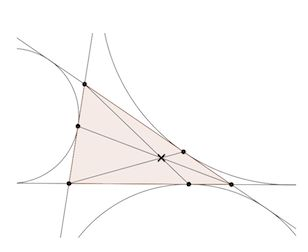 |
X(8) | The Nagel point X(8) is the intersection of the lines connecting each vertex to the touchpoint of the opposite excircle. |
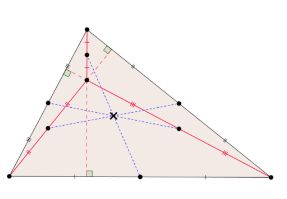 |
X(5) | X(5) is the nine-point center, the center of the famous nine-point circle. The nine points the nine-point circle goes through are the following: The midpoints of AB, BC, CA The feet of the altitudes from A to BC, etc. The midpoints of the segments joining each vertex to the orthocenter. Furthermore, the blue dotted lines are in fact diameters of the nine-point circle, so they meet at its center. |
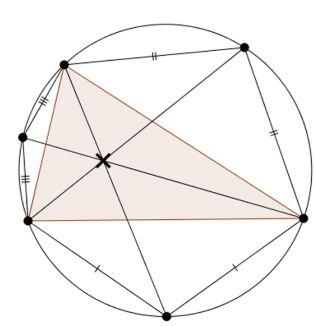 |
X(1) | This diagram constructs the lines joining A with the midpoint of arc BC, B with the midpoint of arc AC, and C with the midpoint of arc AB. These lines are angle bisectors, which meet at the incenter. |
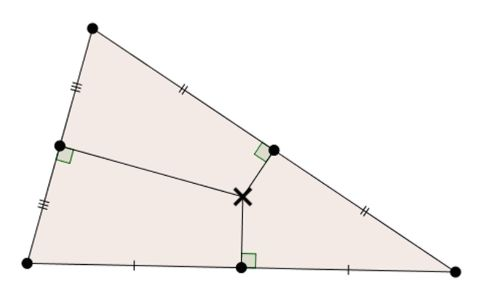 |
X(3) | The circumcenter X(3) is the intersection of perpendicular bisectors of each side. |
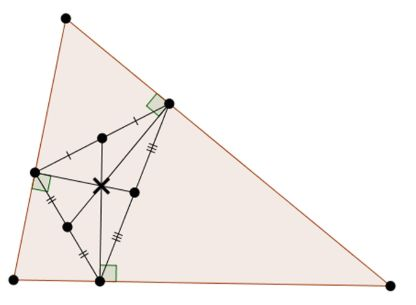 |
X(6) | This is the first diagram that isn’t actually a construction: it starts with the center and shows the property that X is the centroid of its pedal triangle. (The pedal triangle is the triangle constructed by dropping altitudes to each side). The unique triangle center with this property is X(6), the symmedian point. |
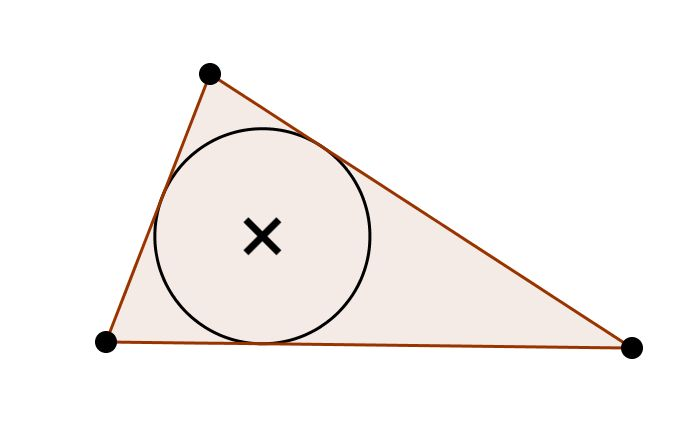 |
X(1) | X(1) is the incenter, the center of the circle inscribed in ABC. |
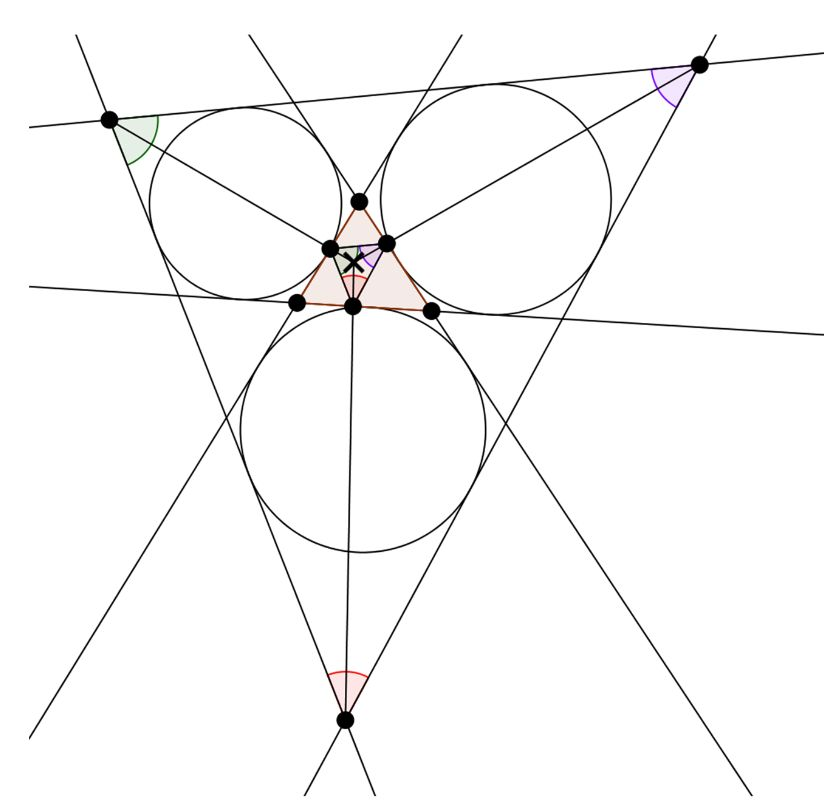 |
X(19) | The Clawson point X(19) is the homothetic center of the extangents triangle, formed by the “other” mutual tangents of the excircles, and the orthic triangle, formed by the feet of the altitudes in a triangle. |
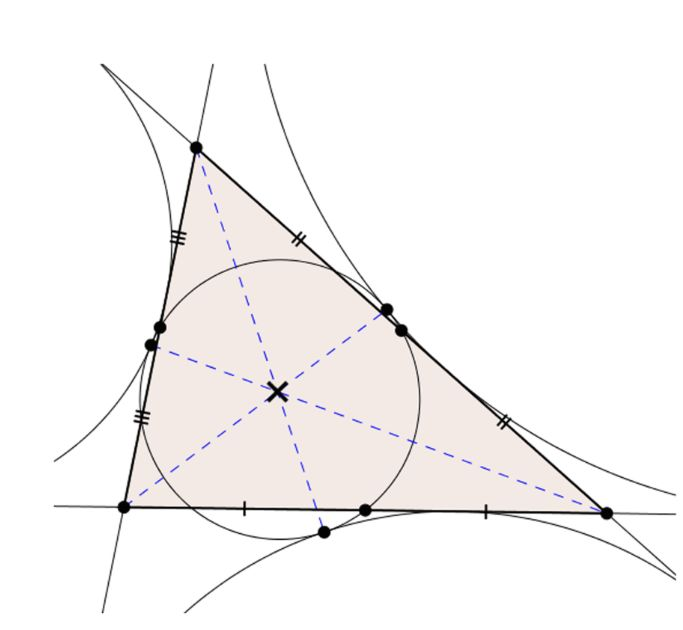 |
X(12) | From ETC: “Let A′B′C′ be the touch points of the nine-point circle with the A-, B-, C- excircles, respectively. The lines AA′, BB′, CC′ concur in X(12).” |
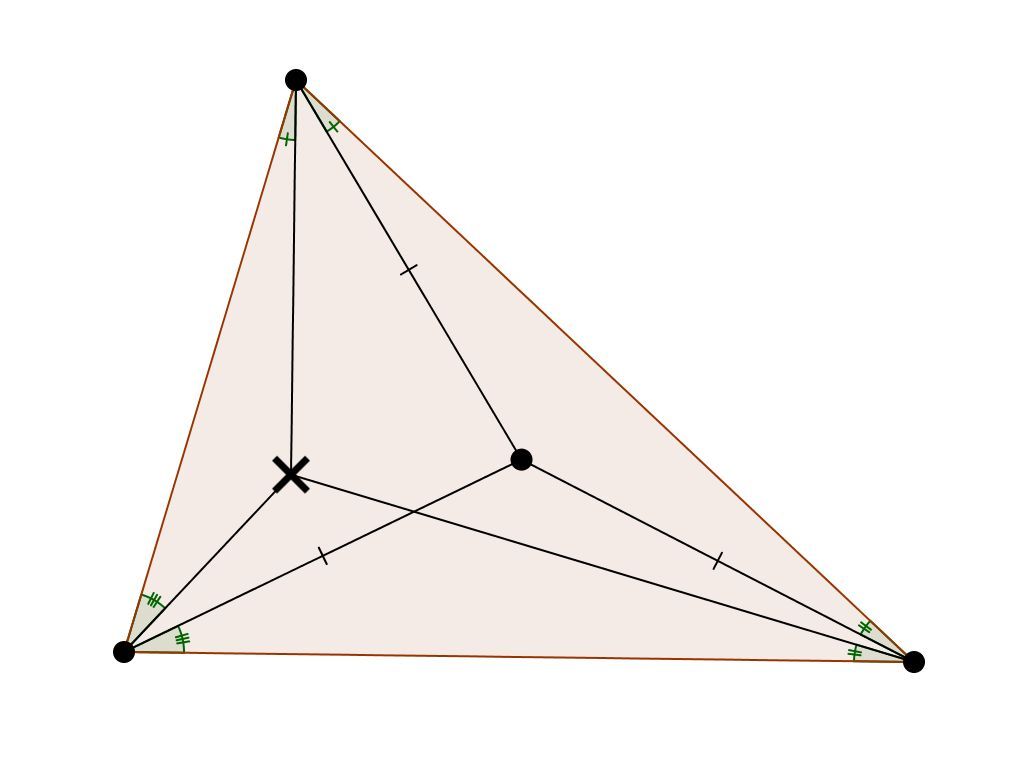 |
X(4) | The orthocenter X(4) is the isogonal conjugate of the circumcenter, meaning it satisfies the angle conditions shown in the diagram. |
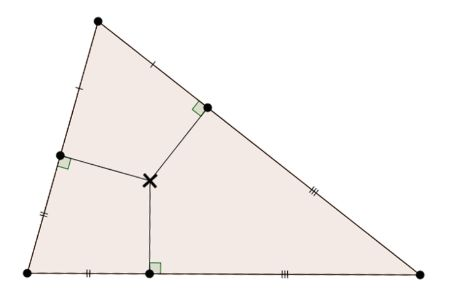 |
X(1) | The depicted points on the sides of the triangle are the touchpoints of the incircle (this is because the length of the tangents from A to the incircle are equal, similarly B, C). The incenter X(1) is the intersection of the perpendiculars from those points to the sides. |
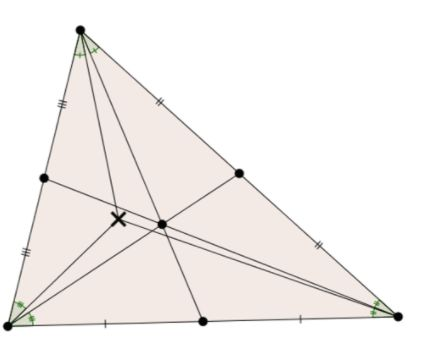 |
X(6) | The symmedian point X(6) is the isogonal conjugate of the centroid, which is the other interior point in the picture. This means that it is the unique point satisfying the angle conditions shown. |
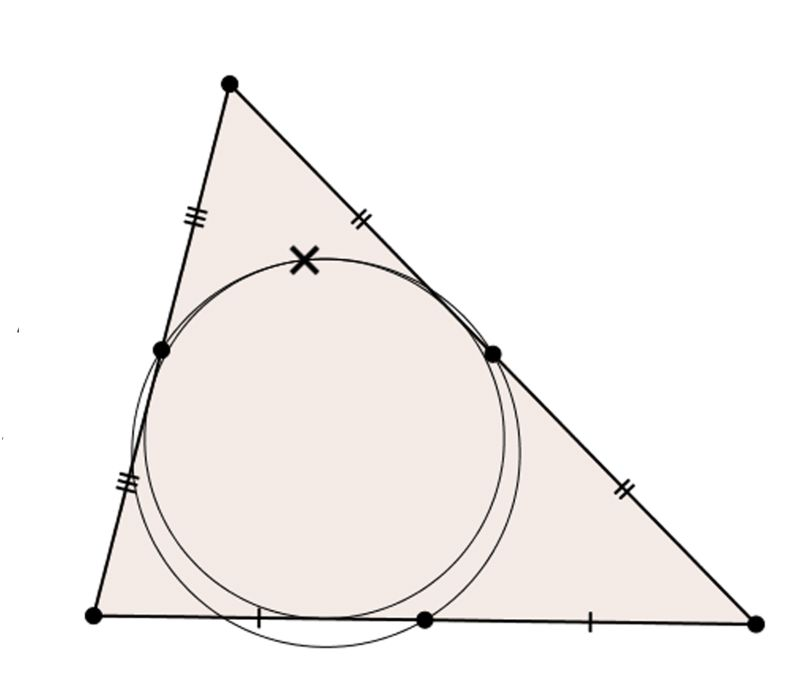 |
X(11) | The Feuerbach point X(11) is the intersection of the incircle and nine-point circle, which are tangent (this is known as Feuerbach’s theorem). The nine-point circle is the circumcircle of the medial triangle (since those are three of the nine points). |
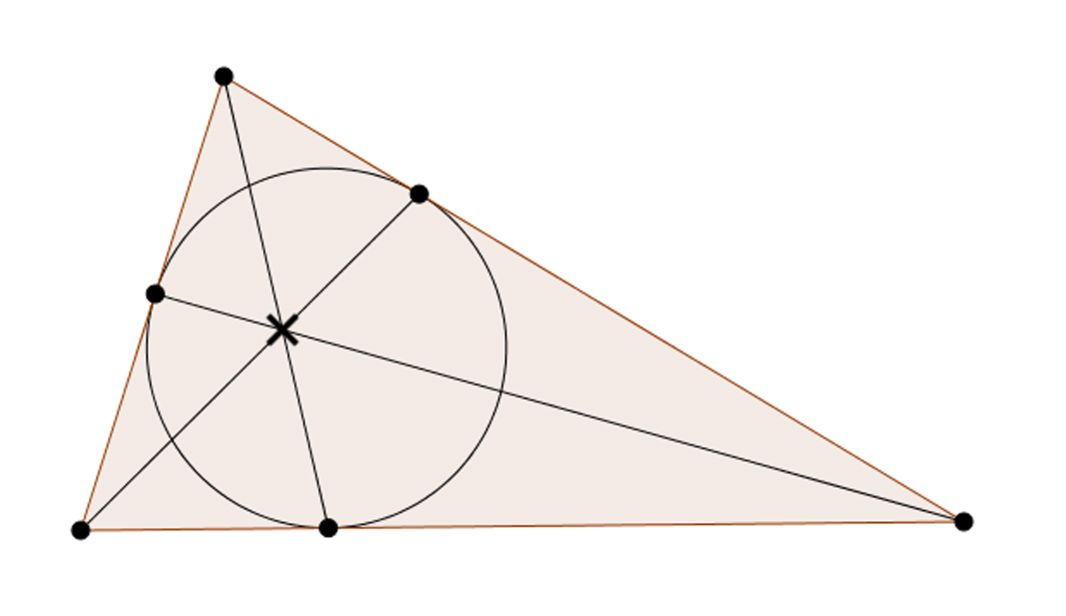 |
X(7) | The Gergonne point X(7) is the intersections of the lines joining each vertex with the opposite touchpoint of the incircle. |
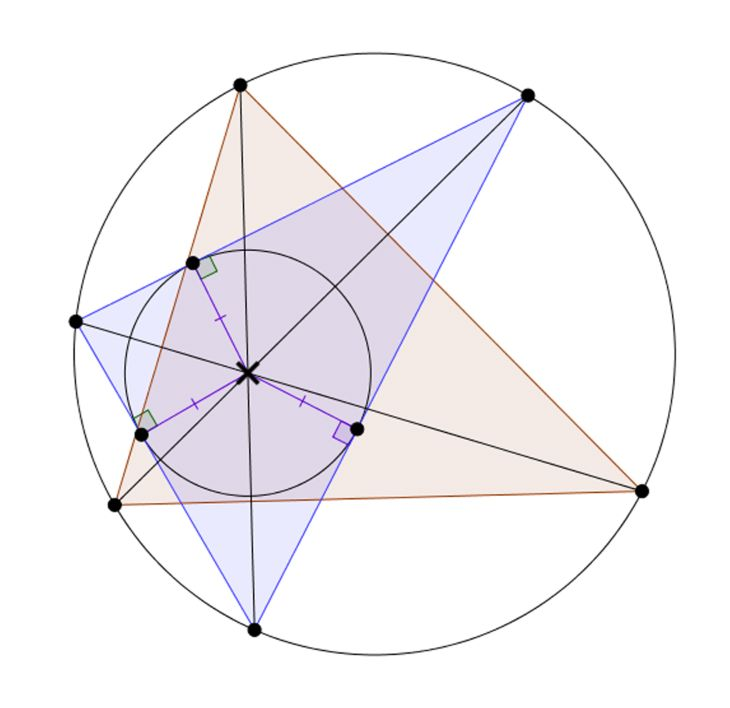 |
X(4) | In the diagram, X is the incenter of the triangle formed by intersecting AX, BX, and CX with the circumcircle. The unique point that satisfies this is X(4). The simplest way to show this is to use the fact that the intersections of AX, BX, CX with the circle are exactly the reflections of H over the sides of the triangle, and that (from ETC) H is the incenter of the orthic triangle. |
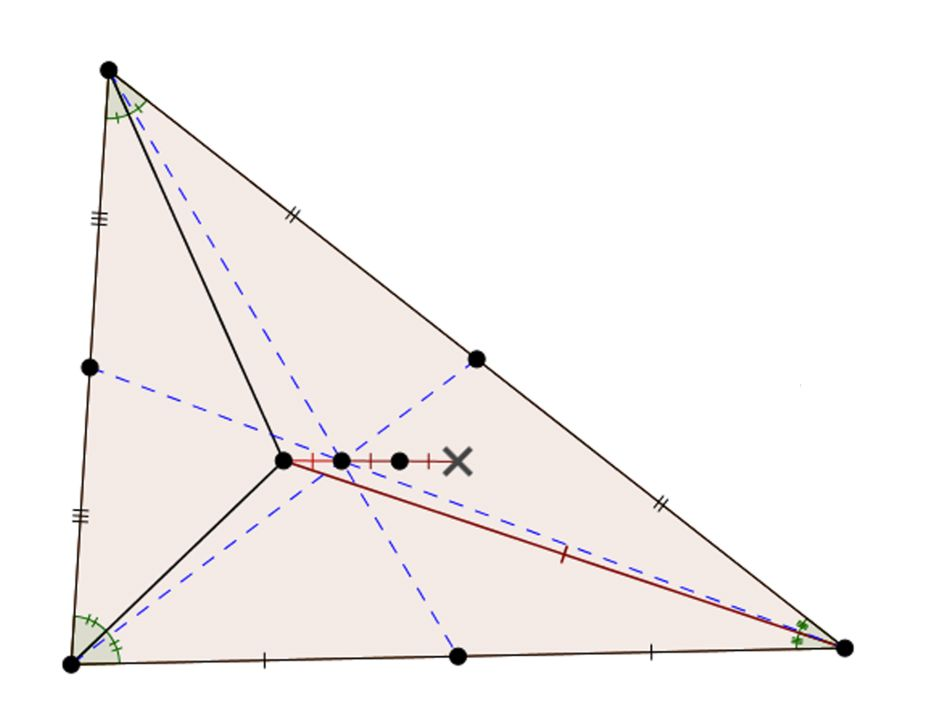 |
X(8) | The Nagel point, X(8), lies on the Nagel line, which goes through the incenter and centroid. If we call those points I and G, respectively, than the Nagel point X satisfies XG=2IG, which is the length relation depicted. |
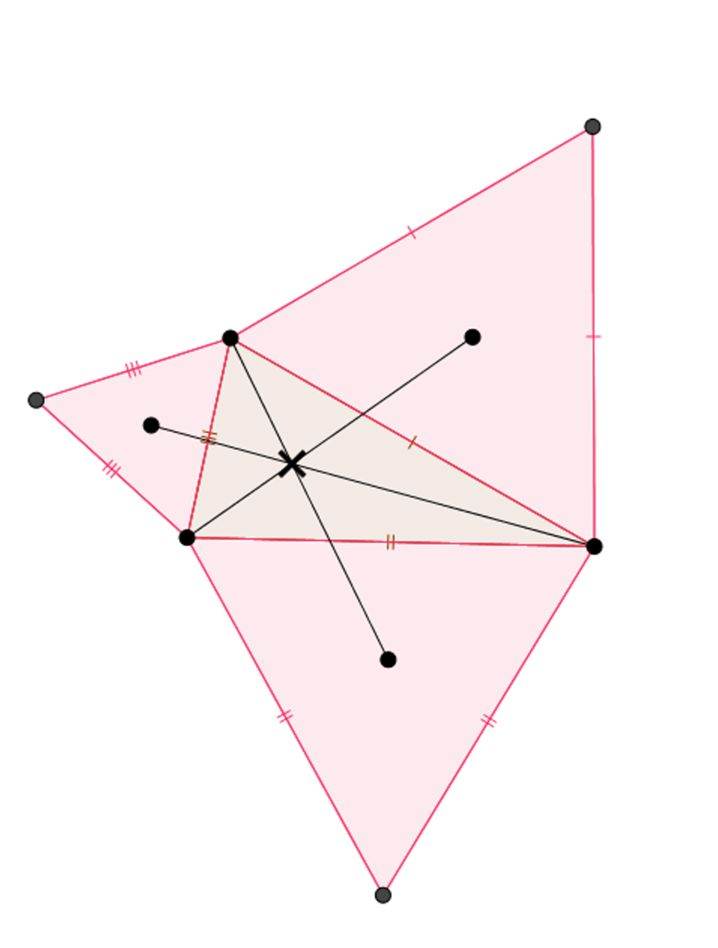 |
X(17) | From ETC: “Let X,Y,Z be the centers of the equilateral triangles in the construction of X(13). The lines AX, BY, CZ concur in X(17).” X(17) is known as the first Napoleon point. |
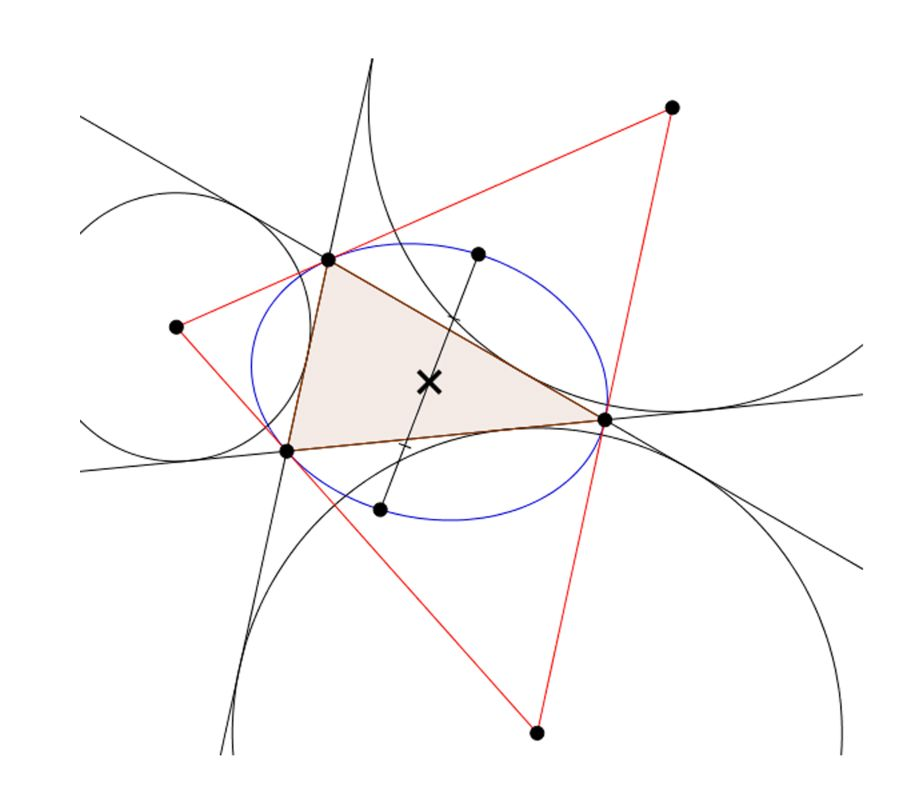 |
X(9) | X(9) is known as the mittenpunkt. This is easily the hardest center to identify: the solver is forced to look in terms of the red triangle formed by the extouch points, and know that the vertices of the original triangle are the feet of the altitudes in that triangle. The orthic inconic is the conic tangent to the sides of a triangle at the feet of the altitudes. Its center is the symmedian point, and finally the symmedian point of the excentral triangle is X(9). |
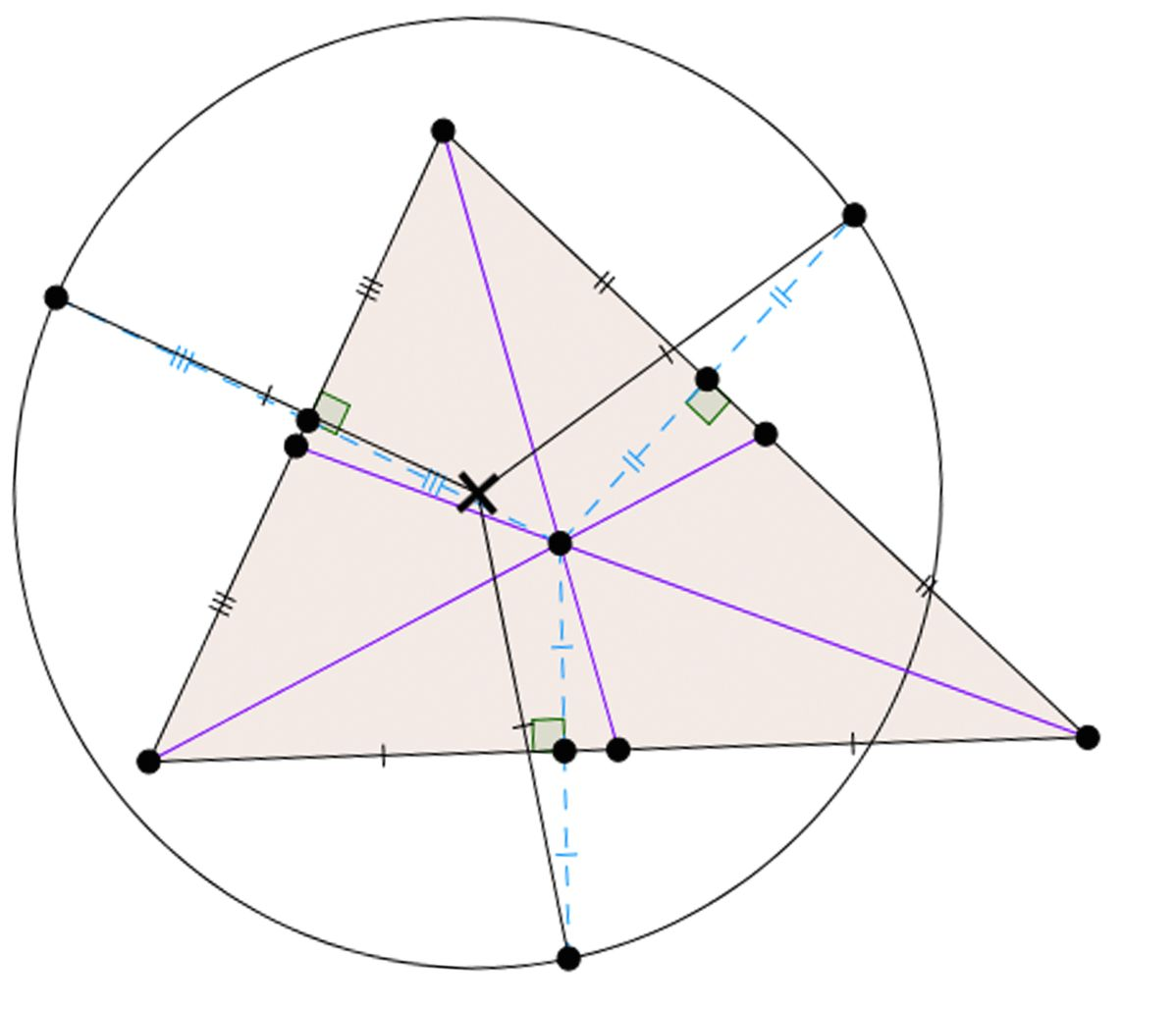 |
X(6) | X(6) is the circumcenter of the triangle formed by the reflections of the centroid over the sides of the triangle. In ETC notation: “X(6) = X(3)-of-reflection-triangle-of-X(2).” |
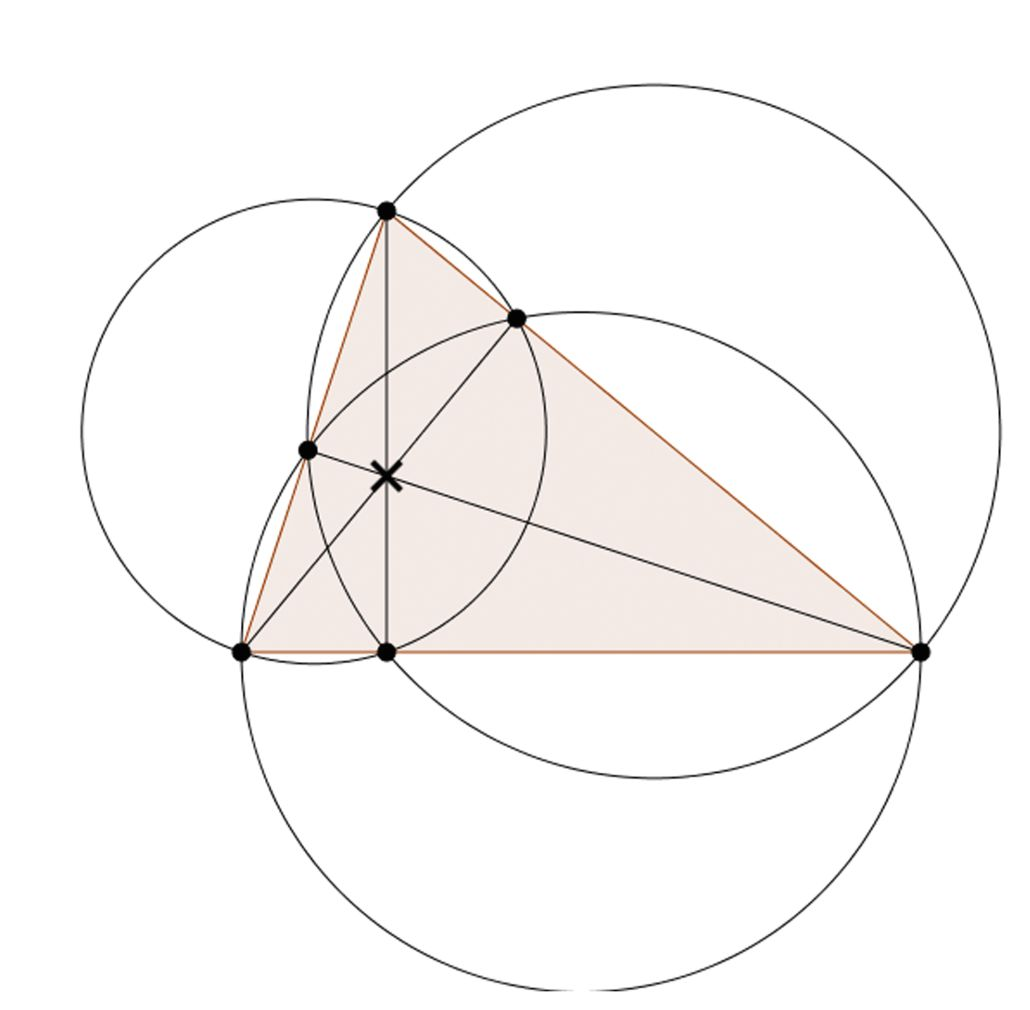 |
X(4) | Let X be the point in the picture, and let D, E, and F be the intersections of AX, BX, and CX with the opposite sides. The picture shows the condition that quadrilaterals BFEC, AEDB, and CDFA are all cyclic. The unique point with this property is X(4), where the circles in question are the circles of diameter BC, AB, and AC, by Thales’ Theorem. |
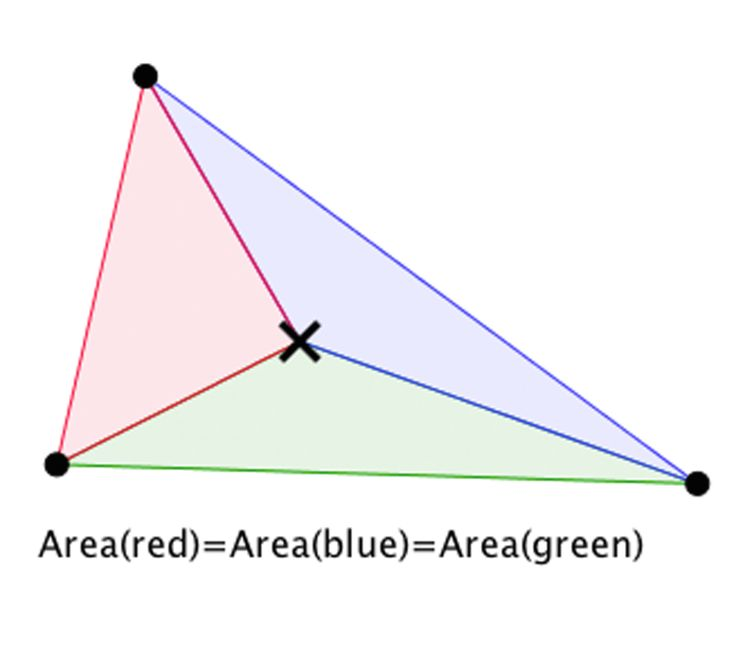 |
X(2) | The picture describes the condition that triangles AXB, BXC, and AXC each have equal area. From ETC: “The triangles BXC, CXA, AXB have equal areas if and only if X = X(2).” |
Having identified all of the triangle centers, it’s possible to compute the equations in each line, using the result to index into the alphabet:
| Equation | Result | Letter |
|---|---|---|
| (10+21−13)÷2 | 9 | I |
| 6(8−5)+1 | 19 | S |
| 3(6−1) | 15 | O |
| 19−12 | 7 | G |
| 4²−1 | 15 | O |
| 6+11−7+4 | 14 | N |
| 8÷(17−9) | 1 | A |
| 6·4÷2 | 12 | L |
Reading the letters spells out ISOGONAL, which clues
to take the isogonal conjugate (an operation of triangle centers,
easily looked up on the ETC) of each point in the
pictures. Translating each center to its isogonal conjugate and
plugging into the same equations yields:
| Equation | Result | Letter |
|---|---|---|
| (58+65−15)÷6 | 18 | R |
| 2(56−54)+1 | 5 | E |
| 4(2−1) | 4 | D |
| 63−60 | 3 | C |
| 3²−1 | 8 | H |
| 2+59−55+3 | 9 | I |
| 56÷(61−57) | 14 | N |
| 2·3÷6 | 1 | A |
The letters in order spell the answer, RED CHINA.