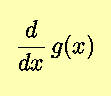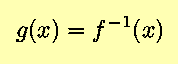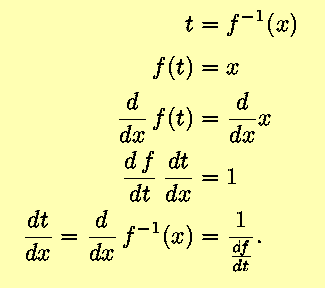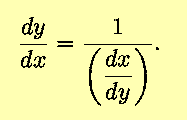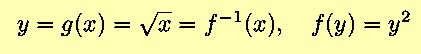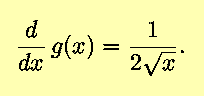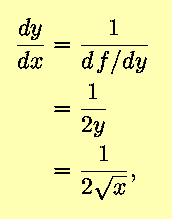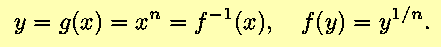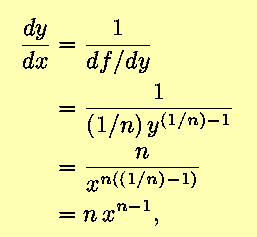Derivatives of Inverse Functions
Suggested Prerequesites:
Inverse Functions,
Implicit Differentiation, Chain Rule
Sometimes it may be more convenient or even necessary to find the derivative
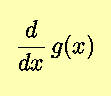based on the knowledge or condition that
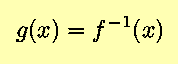for some function f(t), or, in other words, that
g(x) is the inverse of
f(t) = x. Then,
recognizing that t and g(x) represent
the same quantity, and remembering the Chain Rule,
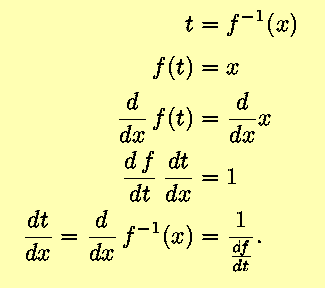Using
Leibniz's fraction notation for derivatives, this result becomes
somewhat obvious;
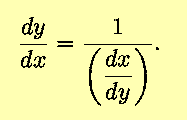As with the chain rule, the
Leibnitz notation can often provide insight that can be confirmed using
the definition of the derivative or
previously proven results.
What the above does not indicate, and which will be shown
via the following examples, is that when the derivative of an
inverse function is desired as a function of (in the above and
following cases) the independent variable x, the derivative
dx/dy must be solved for x
Some examples:
The following examples will be confined to those functions that can be
differentiated by use of the Power Rule and the Chain Rule in
combination.
- First, consider
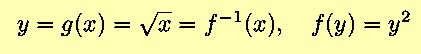We know from the Power Rule, with n=2, that
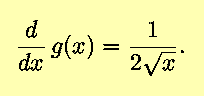Equivalently,
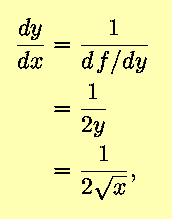as before.
- The above may be generalized; for nonzero n,
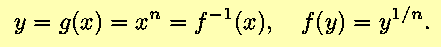Then,
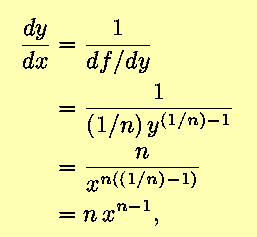in agreement with the Power Rule.
It may seem that the formalism doesn't add much to our toolkit for
differentiation, and indeed, the above examples do not make a great
case for memorizing the rule for differentation of inverse functions.
However, when more complicated functions are considered, the use of
the chain rule and implicit differentiation allows derivatives to be
calculated with relative ease. Examples will be given in the
appropriate sections of this hypertext.
Back to the Calculus page |
Back to the World Web Math Categories Page
watko@mit.edu
Last modified September 30, 1998