 The Notation of Differentiation
The Notation of Differentiation The Notation of Differentiation
The Notation of Differentiation
 A derivative is always the derivative of a function with respect
to a variable. When we write the definition of the derivative as
A derivative is always the derivative of a function with respect
to a variable. When we write the definition of the derivative as
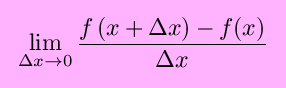
we mean the derivative of the function f(x) with respect to the variable x.
 One type of
notation for derivatives is sometimes called prime
notation. The function f´(x),
which would be read ``f-prime of x'', means the
derivative of f(x) with respect to
x. If we say y = f(x), then
y´ (read ``y-prime'') =
f´(x). This is even sometimes taken as
far as to write things such as, for
y = x4 + 3x
(for example), y´ =
(x4 + 3x)´.
One type of
notation for derivatives is sometimes called prime
notation. The function f´(x),
which would be read ``f-prime of x'', means the
derivative of f(x) with respect to
x. If we say y = f(x), then
y´ (read ``y-prime'') =
f´(x). This is even sometimes taken as
far as to write things such as, for
y = x4 + 3x
(for example), y´ =
(x4 + 3x)´.
 Higher order derivatives in prime notation are
represented by increasing the number of primes. For example, the second
derivative of y with respect to x would be written
as
Higher order derivatives in prime notation are
represented by increasing the number of primes. For example, the second
derivative of y with respect to x would be written
as
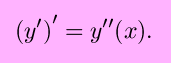
Beyond the second or third derivative, all those primes get messy, so often the order of the derivative is instead writen as a roman superscript in parenthesis, so that the ninth derivative of f(x) with respect to x is written as f(9)(x) or f(ix)(x).
 A second
type of notation for derivatives is sometimes called operator
notation. The operator Dx is
applied to a function in order to perform differentiation. Then, the
derivative of f(x) = y with
respect to x can be written as Dxy
(read ``D -- sub -- x of y'') or as
Dxf(x (read ``D -- sub
x -- of -- f(x)'').
A second
type of notation for derivatives is sometimes called operator
notation. The operator Dx is
applied to a function in order to perform differentiation. Then, the
derivative of f(x) = y with
respect to x can be written as Dxy
(read ``D -- sub -- x of y'') or as
Dxf(x (read ``D -- sub
x -- of -- f(x)''). Higher order derivatives are written by adding a superscript to
Dx, so that, for example the third derivative of
y =
(x2+sin(x))
with respect to x would be written as
Higher order derivatives are written by adding a superscript to
Dx, so that, for example the third derivative of
y =
(x2+sin(x))
with respect to x would be written as
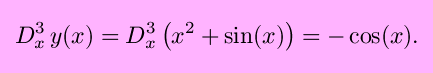
 Another
commonly used notation was developed by
Leibnitz and is accordingly called Leibnitz
notation. With this notation, if
y = f(x), then the
derivative of y with respect to x can be written
as
Another
commonly used notation was developed by
Leibnitz and is accordingly called Leibnitz
notation. With this notation, if
y = f(x), then the
derivative of y with respect to x can be written
as
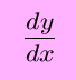
(his is read as ``dy -- dx'', but not ``dy minus dx'' or sometimes ``dy over dx''). Since y = f(x), we can also write
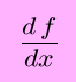
This notation suggests that perhaps derivatives can be treated like fractions, which is true in limited ways in some circumstances. (For example with the chain rule.) This is also called differential notation, where dy and dx are differentials. This notation becomes very useful when dealing with differential equations.
 A variation of Leibnitz's differential notation is written instead as
A variation of Leibnitz's differential notation is written instead as
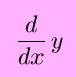
which resembles the above operator notation, with (d/dx as the operator).
 Higher order derivatives using leibnitz notation can be written as
Higher order derivatives using leibnitz notation can be written as
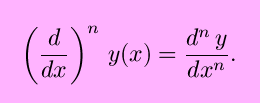
The exponents may seem to be in strange places in the second form, but it makes sense if you look at the first form.
Back to the Calculus page | Back to the World Web Math top page