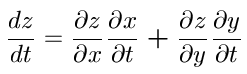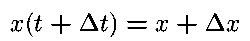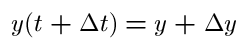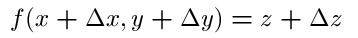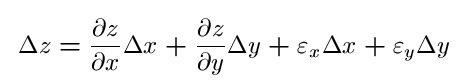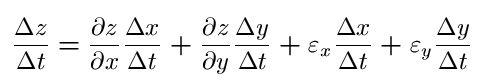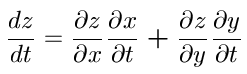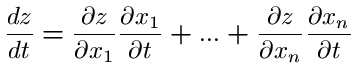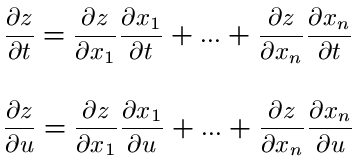The Chain Rule
Prequisites: Partial Derivatives
Back in basic calculus, we learned how to use the chain rule on single variable functions. Now we want to be able to use the chain rule on multi-variable functions.
Lets start with the two-variable function and then generalize from there. Let z=f(x,y) be our two-variable function. Lets say that both x and y can be expressed as functions of another variable t. x=g(t and y=h(t. Then z is a function of t, say z=f[g(t),h(t)] = F(t). Then the formula for the derivative of z with respect to t is
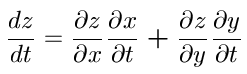
Don't let the fact that I switched notation throw you
Proof
Lets first notice a few things...
Now, by linear approximation we know
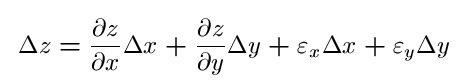
where the above error functions go to zero as delta x and delta y go to zero. We divide by delta t and get,
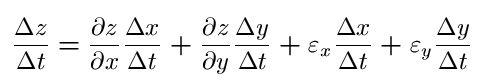
Now as we let delta t go to zero, delta x, delta y, and the error functions go to zero and we get the expression.
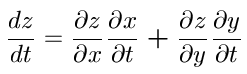
This formula extends as one would expect. If z=f(x1,x2,...xn) and x1 through xn can be expressed as a function of a variable t, then,
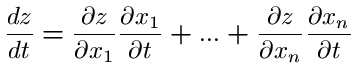
It is not necessary that x1 through xn be only functions of t. They can be functions of other variables, too. Say x1 through xn are functions of two variables t and u. Then the partial derivatives of z are given by
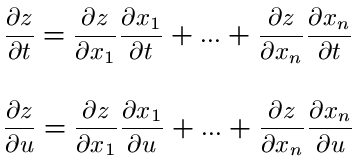
These rules define the chain rules
Vector Calculus Index |
World Web Math Main Page
thing@athena.mit.edu
Last modified 8 August 1997
