Linear Approximations

Linear Approximations for one-variable functions

Lets say f(x) is a one-variable function. Now let P=(c,0) and Q=(d,0) be points on the x-axis, such that f is defined on both P and Q. Let

So we can rewrite,

is the change in the value of f from P to Q. Consider the very familiar quotient

Taking the limit of this quotient as Q approaches P hearkens us back to the definition of taking of a derivative back in basic calculus. This limit, if it exists, gives us the derivative of f at c. In the infant years of calculus, this derivative was not thought of as the rate of change of f but of as a means of getting an approximate value for the change in f when c and the change in x are given. That is the formula,

provides an approximate value for the change in f and is called the linear approximation formula for f at x=c. The constant f'(c) was called the differential coefficient of f at c.

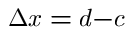
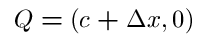
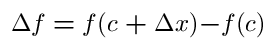
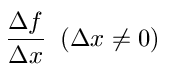
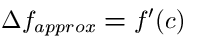
Of course any approximation function also has its error function, which in this case is equal, for any point Q to,

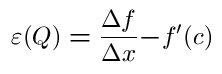
Let's formally define a linear approximation.
Definition: Let f(x) be a one-variable function on a domain D. Let x=c be in D and let P, Q the change in x be defined as above. We say f has a linear approximation at c if, for our chosen c, there is a constant A and an error function of Q, such that:

for all Q in D,

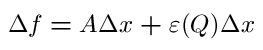
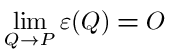
This definition implies

if f has a linear approximation at c, then f is continuous at c.
f has a linear approximation at c if and only if f has a derivative at c.

Linear approximation for multi-variable functions

The definition for linear approximation for a multi-variable function will be (not surprisingly) similar to that of one variable.
Definition: Let f( x₁,x₂,...x_n) be a n-variable function on domain D. Let P be a fixed point in D, P=(a₁,a₂,...a_n). Let Q=((a₁+x₁),(a₂+x₂),...(a_n+x_n)) be another point in D. Let f = f((a₁+x₁),(a₂+x₂),...(a_n+x_n))-f(a₁,a₂,...a_n). We say that f has a linear approximation at P if, for our chosen P, there exist constants A₁,A₂,...A_n and n functions erf₁(Q), erf₂(Q),... erf_n(Q) such that

for all Q in D, f= A₁x₁ + A₂ x₂+...A_nx_n+ erf₁(Q)x₁ + erf₂(Q)x₂ + ... +erf_n(Q)x_n
and as Q approaches P all the error functions of Q go to zero.

This definition implies the following:

If f has linear approximations at P, then f is continuous at P
if f has linear approximations at P, then f has first-order partial derivatives at P and these derivatives have the values of f_x₁(P)=A₁ , f_x₂(P)=A₂ , . . . f_{x_n}(P)=A_n

One must note that it is possible for f to have first-order partial derivatives at every point, but not to have linear approximations at a certain point P in its domain. That is, a f can have first-order partial derivatives at every point, but not be continuous at a certain point P in its domain.

Vector Calculus Index | World Web Math Main Page

thing@athena.mit.edu

Last modified 24 July 1997