|
由前面对於单摆的介绍(请参阅什麽是单摆?周期如何计算?)
我们知道 ,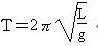
其中T是单摆的周期, L是单摆的长度, g为重力加速度
接下来我们剪一段约一公尺的细线, 并且利用尺测量细线的长度, 以下是站长所测量的数据, 站长先将线段折成两半,
然後测量细线的长度(L/2), 乘以两倍以後就是细线的长度了(d):
|
|
1 |
2 |
3 |
4 |
5 |
平均 |
标准差 |
|
d/2(cm) |
59.9 |
59.8 |
60 |
59.9 |
60 |
59.92 |
0.08 |
|
d(cm) |
119.8 |
119.6 |
120 |
119.8 |
120 |
119.84 |
0.17 |
总共测量了五次, 得到数据为 119.84±0.17公分,
再减去0.5公分(预留用来固定在墙上的部分), 我们得到单摆的长度为 L = 119.34±0.17公分=1.1934±0.0017公尺.
|
接下来我们将硬币用胶带黏在细线上组合成"单摆",
并且将单摆固定在墙上. 右图就是固定好的单摆外观.
在实验器材准备好之後,
轻轻推动硬币使单摆开始来回摆动, 同时按下码表计时.
|
利用铁钉固定
固定好的硬币
|
单摆外观 |
以摆动50次之後按下码表记录时间, 总共做五次求平均. 下是站长在家里面所测得的数据:
|
|
1 |
2 |
3 |
4 |
5 |
平均 |
标准差 |
|
50T (s) |
109.68 |
107.73 |
109.75 |
109.67 |
109.75 |
109.32 |
0.89 |
|
T(s) |
2.194 |
2.155 |
2.195 |
2.193 |
2.195 |
2.186 |
0.018 |
聪明的你一定有发现, 怎麽第二次的数据特别奇怪?
答案是因为站长打了一个哈欠, 数错了. 将数据画成图, 可以看得更清楚:
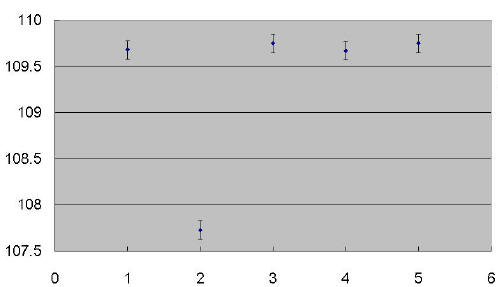
因此我们在完成实验测量之後, 应该要再行检查数据是否有错误, 并且将错误的数据去除後重新做平均:
|
|
1 |
2 |
3 |
4 |
5 |
平均 |
标准差 |
|
50T (s) |
109.68 |
x |
109.75 |
109.67 |
109.75 |
109.71 |
0.04 |
|
T(s) |
2.194 |
x |
2.195 |
2.193 |
2.195 |
2.194 |
0.001 |
因此所得到的单摆周期为 T=2.194±0.001秒
这麽一来, 我们所需要的实验数值T跟L都准备好了.
根据公式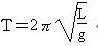,T=2.194±0.001秒
L=1.1934±0.0017公尺
可得 重力加速度 g = 9.785
± 0.014 m/s2
其中 0.014是统计误差.
皆下来我们要了解一下实验仪器的误差, 或称为系统误差.
系统误差告诉我们这套实验仪器到底能够将重力加速度测得多准.
仪器的误差来源主要是对於周期T以及单摆长度L的影响, 我们用来测量单摆长度的遗弃是直尺, 刻度的误差约为0.1公分. 而关於周期的计算,
由於人有所谓的反应时间, 反应时间大约为0.1秒, 因此所计算得到的周期误差约为0.1秒/50 = 0.002秒.
以下为系统误差的计算:
|
|
L的误差 |
T的误差 |
|
误差大小 |
0.1公分 |
0.002秒 |
|
加一个误差量所得g值(m/s2) |
9.767 |
9.793 |
|
(+)差异大小(m/s2) |
-0.018 |
0.008 |
|
减一个误差量所得g值(m/s2) |
9.803 |
9.777 |
|
(-)差异大小(m/s2) |
0.018 |
-0.008 |
因此我们可以大略得到系统误差大小=(0.0182+0.0082)1/2=0.020
(m/s2) 因此站长家里面的重力加速度大小为
9.785
± 0.014
± 0.020
m/s2 是不是跟大家所熟悉的 9.8 m/s2
很接近呢? 这表示站长的家在地球, 而不是在火星. |
光与物质小站首页
/ 力学
/ 重力加速度测量实验
手表或码表 一个