N(x : 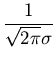 exp exp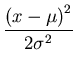
|
(12) |
Even a cursory examination of Figure 3 reveals that the sample frequency distribution is approximately symmetric about a mean value of 320. Moreover, the maximum frequency occurs very close to the mean value. Furthermore, the frequency diminishes rapidly as we move either to the left or to the right of the mean value. These observations suggest the use of a bell shaped distribution to model the data. Or in mathematical terms, we seek to model the population frequency distribution using a Gaussian (normal) distribution. The Gaussian distribution is one of the most widely used probability distributions with applications not only in statistical analysis of data but in theory of probability and stochastic processes. The mathematical expression for the normal distribution is given by
N(x : 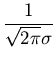 exp exp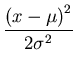
|
(12) |
| (13) | |||
| (14) | |||
| (15) |
Now how can we relate the discrete frequency distribution
of the melting point data
to the continuous normal distribution?
We can rephrase this question as: what is the appropriate
frequency function which will approach
N(x : ![]() ,
,![]() ) in the limit of the interval length
) in the limit of the interval length
![]() x
x ![]() 0
and the number of observations
n
0
and the number of observations
n ![]()
![]() ?
Such a function can be constructed by
suitably scaling fj so that after scaling,
the area under fj vs. Pj curve
is unity. We can then use the scaled fj for comparisons against
N(x :
?
Such a function can be constructed by
suitably scaling fj so that after scaling,
the area under fj vs. Pj curve
is unity. We can then use the scaled fj for comparisons against
N(x : ![]() ,
,![]() ).
).
Now, if we plot a histogram of fj vs. Pj, the contribution to
the area from interval j is
fj![]() x. So the total area from
m intervals is
x. So the total area from
m intervals is
![]() x
x![]() fj = n
fj = n![]() x. Hence, in order
to be consistent with the normalization given by Eq. 13, we should
compare
fj/(n
x. Hence, in order
to be consistent with the normalization given by Eq. 13, we should
compare
fj/(n![]() x) with
N(x :
x) with
N(x : ![]() ,
,![]() ). Such a comparison
for the melting point data is shown in Figure 5. Note that in
Figure 5, the continuous curve corresponds to
n
). Such a comparison
for the melting point data is shown in Figure 5. Note that in
Figure 5, the continuous curve corresponds to
n![]() xN(x :
xN(x : ![]() ,
,![]() ) = 250N(x : 320.1, 6.7) is plotted for
305
) = 250N(x : 320.1, 6.7) is plotted for
305 ![]() x
x ![]() 335 and
the points correspond to fj for
j = 1, 2, ... , 7. As we can
see from Figure 5, the agreement is quite satisfactory, implying
that the distribution of the melting points in the entire population
of alloy parts can be modeled as a Gaussian distribution.
335 and
the points correspond to fj for
j = 1, 2, ... , 7. As we can
see from Figure 5, the agreement is quite satisfactory, implying
that the distribution of the melting points in the entire population
of alloy parts can be modeled as a Gaussian distribution.