In section 2, we computed the number of observations of the melting point within a given interval for 7 intervals and plotted the interval frequency vs. the interval midpoint (refer to Figure 3). Such information obtained by grouping data into various intervals can be used to infer and model how the data is distributed in the entire population. In the context of our example, this means that by studying the statistical properties of the melting point data of the sample grouped into different intervals, we can gain inferences on how the melting point is distributed among the entire population of alloy parts produced.
The first step in this kind of analysis is to define the intervals and
find the frequency of observation within each interval.
Let's say that we chose m intervals of equal length of ![]() x.
Let's denote the mid-points of these
intervals by Pj, for
j = 1, 2, ... , m.
An observation xk
belongs to the interval j if
x.
Let's denote the mid-points of these
intervals by Pj, for
j = 1, 2, ... , m.
An observation xk
belongs to the interval j if
|
Pj - |
(10) |
Once we have collected the interval frequencies, we can compute
the mean and the variance from the grouped data. We will use
the subscript g to denote the statistical measures obtained
from grouped data. In particular,
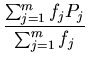 =
= 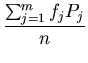 |
|||
| (n - 1) |
(11) |
The cumulative frequency, Fj is defined as the sum of all
the frequencies of the intervals ![]() j. You can compute Fj
recursively as
Fj = Fj - 1 + fj,
j = 2, 3, ... , m with F1 = f1.
Note that Fm = n.
j. You can compute Fj
recursively as
Fj = Fj - 1 + fj,
j = 2, 3, ... , m with F1 = f1.
Note that Fm = n.