


Next: On Sorting Data
Up: Frequency Distribution Revisited
Previous: Modeling the Melting Point
Once we have modeled the data using a distribution, we have at our
disposal a predictive tool to evaluate the probability that
a certain observation can be made between any 2 melting points
xa and xb such that xa < xb. This probability, denoted by
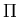 (xa, xb), is
the area under the distribution curve between x = xa and x = xb; i.e.,
(xa, xb), is
the area under the distribution curve between x = xa and x = xb; i.e.,
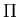 (xa, xb) = (xa, xb) = 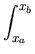 N(x : N(x : 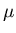 , ,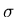 )dx. )dx.
|
(16) |
Note that Eq. 13 is equivalent to the statement that the probability of
making an observation between - 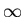 and
and 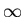 is unity.
is unity.
How do we compute the integral in Eq. 16? First of all, we would like to
define a new variable
which is independent of the units of measurement. Moreover, z = 0 for x = 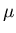 and note that z measures the how far we are away from the mean in units
of the standard deviation.
We now define
the standard normal distribution,
Ns(y : 0, 1)
as
and note that z measures the how far we are away from the mean in units
of the standard deviation.
We now define
the standard normal distribution,
Ns(y : 0, 1)
as
Ns(y : 0,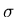 ) = ) = 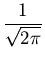 exp(- y2/2). exp(- y2/2).
|
(18) |
Note that the standard normal distribution is a normal distribution
with 0 mean and unit variance.
We now define the standard cumulative distribution function
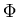 (z) based on
Ns(y : 0, 1) as
However, from Eq. 16, we have
(z) based on
Ns(y : 0, 1) as
However, from Eq. 16, we have
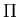 (xa, xb) (xa, xb) |
= |
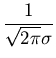 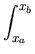 exp exp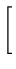 -
- 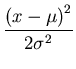
![$\displaystyle \left.\vphantom{-\frac{{(x-\mu)}^2}{2\sigma^2}}\right]$](img42.gif) dx dx |
|
| |
|
= 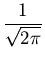 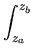 exp(- exp(- 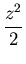 )dz (Note: z = )dz (Note: z = 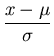 ) ) |
|
| |
|
= 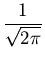 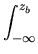 exp(- exp(- 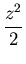 )dz - )dz - 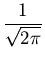 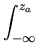 exp(- exp(- 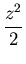 )dz )dz |
|
| |
|
= 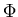 (zb) - (zb) - 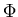 (za). (za). |
(20) |
The values of 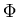 (z) can be found in standard mathematical tables. In maple,
invoke the stats package using with(stats); and do ?statevalf; to get the
syntax of the statevalf function which can be used to evaluate distribution values.
In particular,
statevalf[cdf, normald](value) will give the numerical value of
(z) can be found in standard mathematical tables. In maple,
invoke the stats package using with(stats); and do ?statevalf; to get the
syntax of the statevalf function which can be used to evaluate distribution values.
In particular,
statevalf[cdf, normald](value) will give the numerical value of
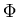 (z) at z = value. It is important to note that
(z) at z = value. It is important to note that
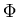 (-
(- 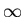 ) = 0,
) = 0,
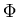 (0) = 1/2 and
(0) = 1/2 and
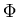 (
(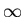 ) = 1. Moreover,
) = 1. Moreover,
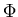 (- z) = 1 - (- z) = 1 - 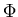 (z). (z).
|
(21) |
See Figure 6 in the maple worksheet figures.ms for a plot of 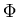 (z).
(z).
The following series formula is also used to compute z, convergence is
slower as the value of z becomes large.
where
| ak |
= |
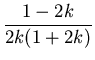 ak - 1, n ak - 1, n 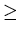 1.
1. |
|
| a0 |
= |
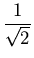 . . |
(23) |
The following is a table which provides, z, 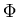 (z) accurate to 6 decimal digits
and the value of k at which the series expansion of Eq. 22 was truncated to obtain
that accuracy. Only z
(z) accurate to 6 decimal digits
and the value of k at which the series expansion of Eq. 22 was truncated to obtain
that accuracy. Only z 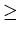 0 need be computed (see Eq. 21).
0 need be computed (see Eq. 21).
0.0 0.500000 0
0.2 0.579260 4
0.4 0.655422 5
0.6 0.725747 6
0.8 0.788145 7
1.0 0.841345 8
1.2 0.884930 9
1.4 0.919243 10
1.6 0.945201 12
1.8 0.964070 13
2.0 0.977250 14
2.2 0.986097 16
2.4 0.991802 17
2.6 0.995339 19
2.8 0.997445 20
3.0 0.998650 22
3.2 0.999313 24
3.4 0.999663 26
3.6 0.999841 28
3.8 0.999928 30
4.0 0.999968 32
4.2 0.999987 35
4.4 0.999995 37
4.6 0.999998 40
4.8 0.999999 42
5.0 1.000000 45
For very large values of z (z > > 1), we may use the asymptotic relation
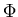 (z) = 1 - exp(- z2/2)/(z (z) = 1 - exp(- z2/2)/(z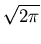 ), ),
|
(24) |
instead of the series expansion given in Eq. 22. For z = 4,
the asymptotic result gives
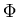 (z) = 0.999966, this is correct to
5 decimal places.
(z) = 0.999966, this is correct to
5 decimal places.
How do we make use of the information in the table above? For instance,
let's ask: what is the probability
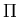 (xa, xb) that an observation is
one standard deviation within the mean? Here,
xa =
(xa, xb) that an observation is
one standard deviation within the mean? Here,
xa = 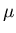 -
- 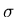 and
xb =
and
xb = 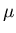 +
+ 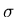 , so that za = - 1 and zb = 1.
So the probability (see Eq. 20)
, so that za = - 1 and zb = 1.
So the probability (see Eq. 20)
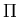 (
(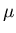 -
- 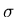 ,
,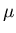 +
+ 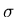 ) =
) = 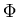 (1) -
(1) - 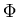 (- 1) = 2
(- 1) = 2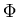 (1) - 1
(1) - 1 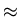 0.6827. This implies that we expect 68.27% of
the entire population
of the alloy parts to have melting points between 313 and 327 if we use
0.6827. This implies that we expect 68.27% of
the entire population
of the alloy parts to have melting points between 313 and 327 if we use
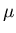 = 320 and
= 320 and 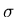 = 7.
Confidence levels are simply probabilities converted into percentages.
For instance, the confidence level of the interval
[
= 7.
Confidence levels are simply probabilities converted into percentages.
For instance, the confidence level of the interval
[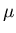 -
- 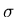 ,
,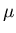 +
+ 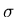 ]
is 68.27% from the probability calculated above.
It can be shown that the probability that an observation x falls within the range
[
]
is 68.27% from the probability calculated above.
It can be shown that the probability that an observation x falls within the range
[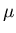 - 1.96
- 1.96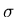 ,
,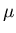 + 1.96
+ 1.96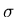 ] is 0.95 for the normal distribution.
So the confidence level for this interval is 95%.
] is 0.95 for the normal distribution.
So the confidence level for this interval is 95%.
The discrete analogue of 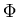 (z) is the cumulative frequency data
scaled with n plotted against
zj = (Pj -
(z) is the cumulative frequency data
scaled with n plotted against
zj = (Pj - 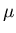 )/
)/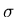 .
We expect Fj/n to approach
.
We expect Fj/n to approach 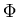 (z) in the
limit
n
(z) in the
limit
n 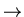
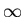 and
and
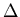 x
x 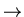 0.
0.



Next: On Sorting Data
Up: Frequency Distribution Revisited
Previous: Modeling the Melting Point
Michael Zeltkevic
1998-04-15
![]() (xa, xb), is
the area under the distribution curve between x = xa and x = xb; i.e.,
(xa, xb), is
the area under the distribution curve between x = xa and x = xb; i.e.,
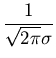
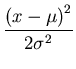
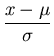 )
)![]() (z) can be found in standard mathematical tables. In maple,
invoke the stats package using with(stats); and do ?statevalf; to get the
syntax of the statevalf function which can be used to evaluate distribution values.
In particular,
statevalf[cdf, normald](value) will give the numerical value of
(z) can be found in standard mathematical tables. In maple,
invoke the stats package using with(stats); and do ?statevalf; to get the
syntax of the statevalf function which can be used to evaluate distribution values.
In particular,
statevalf[cdf, normald](value) will give the numerical value of
![]() (z) at z = value. It is important to note that
(z) at z = value. It is important to note that
![]() (-
(- ![]() ) = 0,
) = 0,
![]() (0) = 1/2 and
(0) = 1/2 and
![]() (
(![]() ) = 1. Moreover,
) = 1. Moreover,
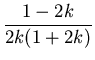 ak - 1, n
ak - 1, n ![]() (xa, xb) that an observation is
one standard deviation within the mean? Here,
xa =
(xa, xb) that an observation is
one standard deviation within the mean? Here,
xa = ![]() -
- ![]() and
xb =
and
xb = ![]() +
+ ![]() , so that za = - 1 and zb = 1.
So the probability (see Eq. 20)
, so that za = - 1 and zb = 1.
So the probability (see Eq. 20)
![]() (
(![]() -
- ![]() ,
,![]() +
+ ![]() ) =
) = ![]() (1) -
(1) - ![]() (- 1) = 2
(- 1) = 2![]() (1) - 1
(1) - 1 ![]() 0.6827. This implies that we expect 68.27% of
the entire population
of the alloy parts to have melting points between 313 and 327 if we use
0.6827. This implies that we expect 68.27% of
the entire population
of the alloy parts to have melting points between 313 and 327 if we use
![]() = 320 and
= 320 and ![]() = 7.
Confidence levels are simply probabilities converted into percentages.
For instance, the confidence level of the interval
[
= 7.
Confidence levels are simply probabilities converted into percentages.
For instance, the confidence level of the interval
[![]() -
- ![]() ,
,![]() +
+ ![]() ]
is 68.27% from the probability calculated above.
It can be shown that the probability that an observation x falls within the range
[
]
is 68.27% from the probability calculated above.
It can be shown that the probability that an observation x falls within the range
[![]() - 1.96
- 1.96![]() ,
,![]() + 1.96
+ 1.96![]() ] is 0.95 for the normal distribution.
So the confidence level for this interval is 95%.
] is 0.95 for the normal distribution.
So the confidence level for this interval is 95%.
![]() (z) is the cumulative frequency data
scaled with n plotted against
zj = (Pj -
(z) is the cumulative frequency data
scaled with n plotted against
zj = (Pj - ![]() )/
)/![]() .
We expect Fj/n to approach
.
We expect Fj/n to approach ![]() (z) in the
limit
n
(z) in the
limit
n ![]()
![]() and
and
![]() x
x ![]() 0.
0.