Transfer Calculations
  Hohman Transfer
  Free Return Trajectory
  Spiral
  Summary of Numerical Data

Launch Windows
  Calculations
  Possible Launch Dates
  Graphical Comparison

Sources

Our best option to get to Mars, the Hohman Transfer, balances time of flight and fuel expenditure. The calculations below are to determine the changes in velocity needed to get the spacecraft out of Earth orbit and into Mars orbit. These values can then be converted directly into fuel amounts and costs.
 
 

Definition of Variables

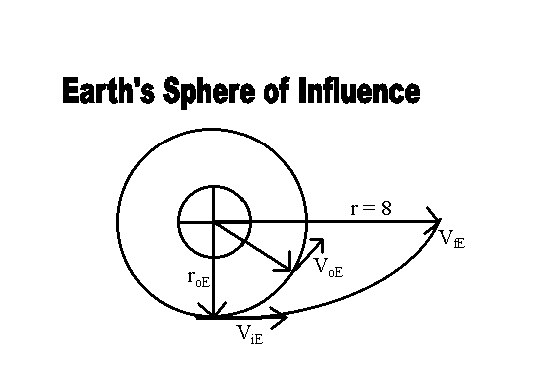
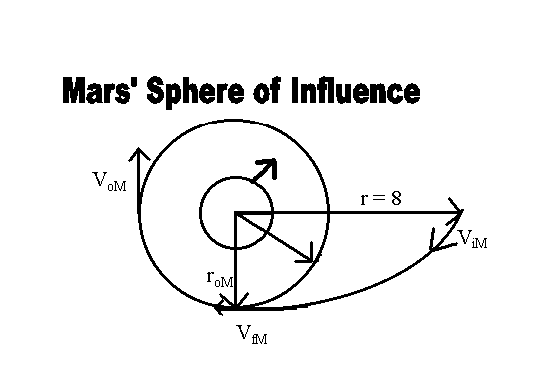
Where

Assumptions made to Simplify Math

Earth and Mars move in circular orbits in the same plane. (In reality, the planes are separated by about 1.8° and Mars' orbit is slightly eliptical).

Earth, Mars, and the Sun are the only gravitationally influential bodies. (In reality, perturbations due to other planets would have a slight effect).

The gravitational effects of these three bodies can be divided into three spheres of influence, in each of which one body is dominant and the others are negligible.

Overview of the Problem

The spacecraft begins in Low Earth Orbit (LEO), with VoE. Thrusters are fired to produce some change in velocity, "delta V." This launches the craft into a hyperbolic escape from Earth with some new ViE. At effectively infinite distance from Earth (once the gravitational pull from Earth is negligible), it is traveling with velocity VfE relative to Earth, or Vp relative to the Sun.

The spacecraft follows an elliptical path from Earth's orbit about the Sun to Mars' orbit, which it reaches at aphelion, just as Mars is approaching that point in its orbit with its own velocity VM.

At this point of intersection, Mars' gravity dominates and the spacecraft approaches Mars on a hyperbolic trajectory from an effectively infinite distance. Its velocity is ViM, relative to Mars. Its final destination is the geosynchronous orbit, which it reaches with a velocity VfM.

Once at the right orbit, the ship fires engines to produce another change in velocity, "delta V-2," slowing it down to VoM. The ship is now in stable orbit.

Setting up the Problem

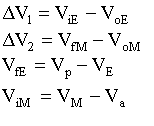
Since occurences at Mars and at Earth are basically the same and every step is reversible, the return transfer has "delta V-2" to leave Mars and "delta V-1" to enter orbit about Earth.

Constants:

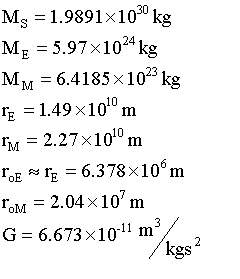
Note: RoM is derived at the end of this page.

Calculations

Conservation of energy ultimately leads to the equation

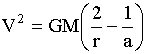
For the Sun's Sphere of influence, assuming circular orbits of planets,

,

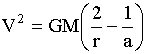
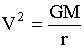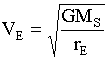and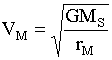 

For a Hohman Transfer elipse, 

,

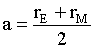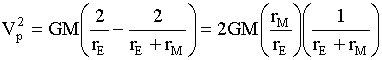
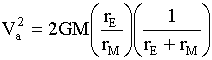
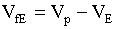
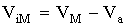
For Earth's sphere of influence, where r = infinity,

,

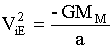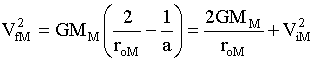
Again assuming a circular orbit,

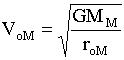
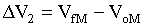
Substitute for Constant Values to Solve Equations

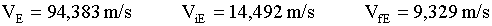
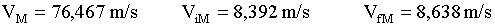
Therefore

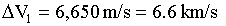
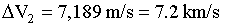
Now find 

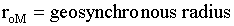
T=rotational period of Mars. Assume gravitational force is equal to a centripetal force.

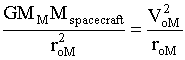
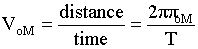
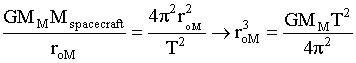
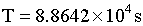
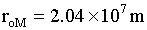
References:
Kelppner, Daniel and Kolenkow, Robert J. An Introduction To Mechanics. McGraw Hill, Inc., Boston: 1973.
Mars Academy. www.marsacademy.com. 4/10/2000.