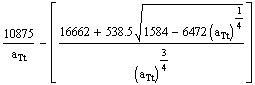Transfer
Calculations
Hohman
Transfer
Free
Return Trajectory
Spiral
Summary
of Numerical Data
Launch
Windows
Calculations
Possible
Launch Dates
Graphical
Comparison
Sources
This problem is especially complex because force is continually
added to the system. Because conservation of energy does not apply, there
is no closed-form analytical solution to the spiral trajectory. With a
few assumptions, however, the trajectory can be modeled. There are multiple
approaches to the problem. This report follows the approach suggested
by MIT Aero/Astro Professor Richard Battin. We assume the following: that
acceleration due to thrust from the engines is constant and in the direction
perpendicular to the direction of motion, and that perturbations due to
the influence of the Van Allen radiation belts are negligible. Definitions of Variables Calculations Orbit of Earth: = Orbit around the sun: Orbit around Mars: Total time as a function of thrust acceleration: References: Battin, Richard H. An Introduction to
the Mathematics and Methods of Astrodynamics. New York: American Institute
of Aeronautics and Astronautics, 1987.
= thrust acceleration 
=velocity of initial circular
orbit around a large mass (either Earth or Mars or the Sun)
= initial
radius of orbit
=
= 
=
= 
= 
= 
=
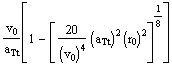
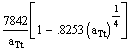
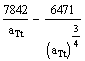
semimajor axis = 
m
= 
= 
= 
=
= 
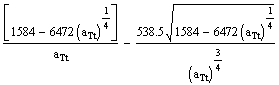
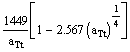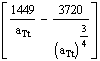
