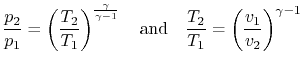Subsections
2.4 Specific Heats: the relation between temperature change and heat
[VW, S& B: 5.6]
How much does a given amount of heat transfer change the temperature
of a substance? It depends on the substance. In general
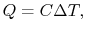 |
(2..4) |
where 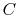 is a constant that depends on the substance. We can
determine the constant for any substance if we know how much heat is
transferred. Since heat is path dependent, however, we must specify
the process, i.e., the path, to find
is a constant that depends on the substance. We can
determine the constant for any substance if we know how much heat is
transferred. Since heat is path dependent, however, we must specify
the process, i.e., the path, to find 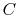 .
.
Two useful processes are constant pressure and constant volume, so
we will consider these each in turn. We will call the specific heat
at constant pressure 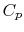 , and that at constant volume
, and that at constant volume 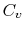 , or
, or
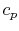 and
and 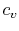 per unit mass.
per unit mass.
- The Specific Heat at Constant Volume
Remember that if we specify any two properties of the system, then
the state of the system is fully specified. In other words we can
write
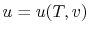 ,
, 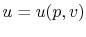 or
or 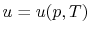 . [VW, S & B: 5.7]
. [VW, S & B: 5.7]
Consider the form
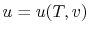 , and use the chain rule to write how
, and use the chain rule to write how
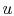 changes with respect to
changes with respect to 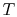 and
and 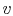 :
:
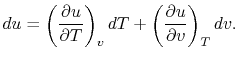 |
(2..5) |
For a constant volume process, the second term is zero since there
is no change in volume, 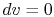 . Now if we write the First Law for
a quasi-static process, with
. Now if we write the First Law for
a quasi-static process, with 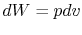 ,
,
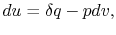 |
(2..6) |
we see that again the second term is zero if the process is also
constant volume. Equating (2.5) and
(2.6) with 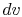 canceled in each,
canceled in each,
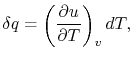 |
|
and rearranging
|
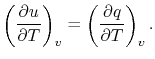 |
|
In this case, any energy increase is due only to energy transfer as
heat. We can therefore use our definition of specific heat from
Equation (2.4) to define the specific
heat for a constant volume process,
- The Specific Heat at Constant Pressure
If we write 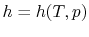 , and consider a constant pressure process, we
can perform a similar derivation to the one above and show that
, and consider a constant pressure process, we
can perform a similar derivation to the one above and show that
In the derivation of 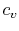 , we considered only a constant volume
process, hence the name, ``specific heat at constant volume.'' It is
more useful, however, to think of
, we considered only a constant volume
process, hence the name, ``specific heat at constant volume.'' It is
more useful, however, to think of 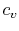 in terms of its definition
as a certain partial derivative, which is a thermodynamic property,
rather than as a quantity related to heat transfer in a special
process. In fact, the derivatives above are defined at any
point in any quasi-static process whether that process is constant
volume, constant pressure, or neither. The names ``specific heat
at constant volume'' and ``specific heat at constant pressure'' are
therefore unfortunate misnomers;
in terms of its definition
as a certain partial derivative, which is a thermodynamic property,
rather than as a quantity related to heat transfer in a special
process. In fact, the derivatives above are defined at any
point in any quasi-static process whether that process is constant
volume, constant pressure, or neither. The names ``specific heat
at constant volume'' and ``specific heat at constant pressure'' are
therefore unfortunate misnomers; 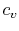 and
and 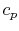 are thermodynamic
properties of a substance, and by definition depend only the state.
They are extremely important values, and have been experimentally
determined as a function of the thermodynamic state for an enormous
number of simple compressible substances2.1.
are thermodynamic
properties of a substance, and by definition depend only the state.
They are extremely important values, and have been experimentally
determined as a function of the thermodynamic state for an enormous
number of simple compressible substances2.1.
To recap:
or
Practice Questions
Throw an object from the top tier of the lecture hall to
the front of the room. Estimate how much the temperature of the room
has changed as a result. Start by listing what information you need
to solve this problem.
The equation of state for an ideal gas is
where 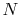 is the number of moles of gas in the volume
is the number of moles of gas in the volume 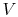 . Ideal gas
behavior furnishes an extremely good approximation to the behavior
of real gases for a wide variety of aerospace applications. It
should be remembered, however, that describing a substance as an
ideal gas constitutes a model of the actual physical
situation, and the limits of model validity must always be kept in
mind.
. Ideal gas
behavior furnishes an extremely good approximation to the behavior
of real gases for a wide variety of aerospace applications. It
should be remembered, however, that describing a substance as an
ideal gas constitutes a model of the actual physical
situation, and the limits of model validity must always be kept in
mind.
One of the other important features of an ideal gas is that its
internal energy depends only upon its temperature. (For now, this
can be regarded as another aspect of the model of actual systems
that the ideal gas represents, but it can be shown that this is a
consequence of the form of the equation of state.) Since 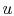 depends
only on
depends
only on 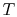 ,
,
In the above equation we have indicated that 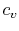 can depend on
can depend on
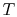 . Like the internal energy, the enthalpy is also only dependent
on
. Like the internal energy, the enthalpy is also only dependent
on 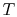 for an ideal gas. (If
for an ideal gas. (If 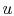 is a function of
is a function of 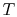 , then, using
the ideal gas equation of state,
, then, using
the ideal gas equation of state, 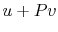 is also.)
Therefore,
is also.)
Therefore,
If we are interested in finite changes of internal energy or
enthalpy, we integrate,
and
Over small temperature changes (
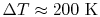 ),
it is often assumed that
),
it is often assumed that 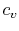 and
and 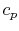 are constant. Furthermore,
there are wide ranges over which specific heats do not vary greatly
with respect to temperature, as shown in SB&VW Figure 5.11. It is
thus often useful to treat them as constant. If so
are constant. Furthermore,
there are wide ranges over which specific heats do not vary greatly
with respect to temperature, as shown in SB&VW Figure 5.11. It is
thus often useful to treat them as constant. If so
These equations are useful in calculating internal energy or
enthalpy differences, but it should be remembered that they hold
only if the specific heats are constant.
We can relate the specific heats of an ideal gas to its gas constant
as follows. We write the first law in terms of internal energy,
and assume a quasi-static process so that we can also write it in
terms of enthalpy, as in
Section 2.3.4,
Equating the two first law expressions above, and assuming an ideal
gas, we obtain
Combining terms,
Since 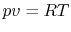 ,
,
An expression that will appear often is the ratio of specific heats,
which we will define as
Below we summarize the important results for all ideal gases, and
give some values for specific types of ideal gases.
- All ideal gases:
- The specific heat at constant volume (
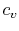 for a unit mass or
for a unit mass or 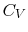 for one kmol) is a function of
for one kmol) is a function of 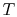 only.
only.
- The specific heat at constant pressure (
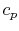 for a unit mass or
for a unit mass or 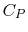 for one kmol) is a function of
for one kmol) is a function of 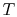 only.
only.
- A relation that connects the specific heats
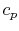 ,
, 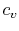 , and the gas constant is
, and the gas constant is
where the units depend on the mass considered. For a unit
mass of gas, e.g., a kilogram, 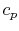 and
and 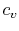 would be the
specific heats for one kilogram of gas and
would be the
specific heats for one kilogram of gas and 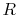 is as defined above.
For one kmol of gas, the expression takes the form
is as defined above.
For one kmol of gas, the expression takes the form
where 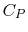 and
and 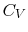 have been used to denote the specific heats
for one kmol of gas and
have been used to denote the specific heats
for one kmol of gas and
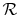 is the universal gas
constant.
is the universal gas
constant.
- The specific heat ratio,
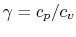 (or
(or 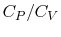 ), is a function of
), is a function of 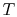 only and is greater than unity.
only and is greater than unity.
- An ideal gas with specific heats independent of temperature,
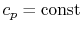 and
and
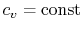 , is referred to as a perfect gas. For example, monatomic gases
and diatomic gases at ordinary temperatures are considered perfect
gases. To make this distinction the terminology "a perfect gas with
constant specific heats" is used throughout the notes. In some
textbooks perfect gases are sometimes also referred to as ideal
gases, and to avoid confusion we use the stated
terminology2.2.
, is referred to as a perfect gas. For example, monatomic gases
and diatomic gases at ordinary temperatures are considered perfect
gases. To make this distinction the terminology "a perfect gas with
constant specific heats" is used throughout the notes. In some
textbooks perfect gases are sometimes also referred to as ideal
gases, and to avoid confusion we use the stated
terminology2.2.
- Monatomic gases, such as He, Ne, Ar, and most metallic vapors:
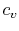 (or
(or 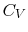 ) is constant over a wide temperature range and is very nearly equal to
) is constant over a wide temperature range and is very nearly equal to 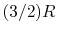 [or
[or
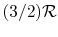 , for one kmol].
, for one kmol].
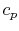 (or
(or 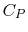 ) is constant over a wide temperature range and is very nearly equal to
) is constant over a wide temperature range and is very nearly equal to 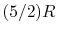 [or
[or
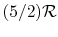 , for one kmol].
, for one kmol].
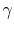 is constant over a wide temperature range and is very nearly equal to
is constant over a wide temperature range and is very nearly equal to 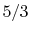 [
[
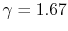 ].
].
- So-called permanent diatomic gases, namely H
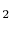 , O
, O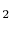 , N
, N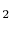 ,
Air, NO, and CO:
,
Air, NO, and CO:
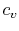 (or
(or 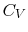 ) is nearly constant at ordinary temperatures, being approximately
) is nearly constant at ordinary temperatures, being approximately 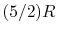 [
[
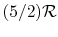 ,
for one kmol], and increases slowly at higher temperatures.
,
for one kmol], and increases slowly at higher temperatures.
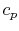 (or
(or 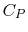 ) is nearly constant at ordinary temperatures, being approximately
) is nearly constant at ordinary temperatures, being approximately 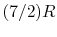 [
[
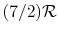 ,
for one kmol], and increases slowly at higher temperatures.
,
for one kmol], and increases slowly at higher temperatures.
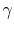 is constant over a temperature range of roughly
is constant over a temperature range of roughly
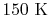 to
to
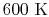 and is very nearly equal to
and is very nearly equal to 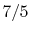 [
[
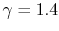 ]. It decreases with temperature above this.
]. It decreases with temperature above this.
- Polyatomic gases and gases that are chemically active, such as CO
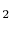 , NH
, NH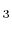 , CH
, CH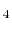 , and Freons:
, and Freons:
The specific heats, 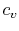 and
and 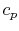 , and
, and 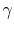 vary with the
temperature, the variation being different for each gas. The general
trend is that heavy molecular weight gases (i.e., more complex gas
molecules than those listed in 2 or 3), have values of
vary with the
temperature, the variation being different for each gas. The general
trend is that heavy molecular weight gases (i.e., more complex gas
molecules than those listed in 2 or 3), have values of 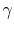 closer to unity than diatomic gases, which, as can be seen above,
are closer to unity than monatomic gases. For example, values of
closer to unity than diatomic gases, which, as can be seen above,
are closer to unity than monatomic gases. For example, values of
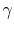 below 1.2 are typical of Freons which have molecular
weights of over one hundred.2.3
below 1.2 are typical of Freons which have molecular
weights of over one hundred.2.3
In general, for substances other than ideal gases, 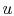 and
and 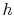 depend on pressure as well as on temperature, and the above
relations will not all apply. In this respect, the ideal gas is a
very special model.
depend on pressure as well as on temperature, and the above
relations will not all apply. In this respect, the ideal gas is a
very special model.
In summary, the specific heats are thermodynamic properties and can
be used even if the processes are not constant pressure or constant
volume. The simple relations between changes in energy (or enthalpy)
and temperature are a consequence of the behavior of an ideal gas,
specifically the dependence of the energy and enthalpy on
temperature only, and are not true for more complex
substances.2.4
2.4.2 Reversible adiabatic processes for an ideal gas
From the first law, with 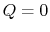 ,
,
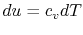 , and
, and
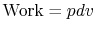 ,
,
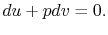 |
(2..7) |
Also, using the definition of enthalpy,
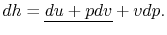 |
(2..8) |
The underlined terms are zero for an adiabatic process. Rewriting
(2.7) and (2.8),
Combining the above two equations we obtain
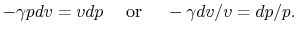 |
(2..9) |
Equation (2.9) can be integrated between states 1 and 2
to give
For an ideal gas undergoing a reversible, adiabatic
process, the relation between pressure and volume is thus:
We can substitute for 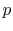 or
or 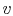 in the above result using the ideal
gas law, or carry out the derivation slightly differently, to also
show that
in the above result using the ideal
gas law, or carry out the derivation slightly differently, to also
show that
We will use the above equations to relate pressure and temperature
to one another for quasi-static adiabatic processes (for instance,
this type of process is our idealization of what happens in
compressors and turbines).
Practice Questions
- On a
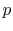 -
-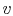 diagram for a closed-system sketch the
thermodynamic paths that the system would follow if expanding from
diagram for a closed-system sketch the
thermodynamic paths that the system would follow if expanding from
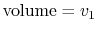 to
to
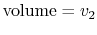 by isothermal and
quasi-static, adiabatic processes.
by isothermal and
quasi-static, adiabatic processes.
- For which process is the most
work done by the system?
- For which process is there heat exchange?
Is it added or removed?
- Is the final state of the system the same
after each process?
- Derive expressions for the work done by the
system for each process.
UnifiedTP
|


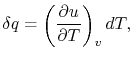
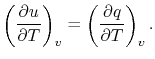
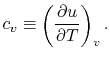
![]() , and consider a constant pressure process, we
can perform a similar derivation to the one above and show that
, and consider a constant pressure process, we
can perform a similar derivation to the one above and show that
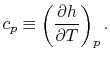
![]() , we considered only a constant volume
process, hence the name, ``specific heat at constant volume.'' It is
more useful, however, to think of
, we considered only a constant volume
process, hence the name, ``specific heat at constant volume.'' It is
more useful, however, to think of ![]() in terms of its definition
as a certain partial derivative, which is a thermodynamic property,
rather than as a quantity related to heat transfer in a special
process. In fact, the derivatives above are defined at any
point in any quasi-static process whether that process is constant
volume, constant pressure, or neither. The names ``specific heat
at constant volume'' and ``specific heat at constant pressure'' are
therefore unfortunate misnomers;
in terms of its definition
as a certain partial derivative, which is a thermodynamic property,
rather than as a quantity related to heat transfer in a special
process. In fact, the derivatives above are defined at any
point in any quasi-static process whether that process is constant
volume, constant pressure, or neither. The names ``specific heat
at constant volume'' and ``specific heat at constant pressure'' are
therefore unfortunate misnomers; ![]() and
and ![]() are thermodynamic
properties of a substance, and by definition depend only the state.
They are extremely important values, and have been experimentally
determined as a function of the thermodynamic state for an enormous
number of simple compressible substances2.1.
are thermodynamic
properties of a substance, and by definition depend only the state.
They are extremely important values, and have been experimentally
determined as a function of the thermodynamic state for an enormous
number of simple compressible substances2.1.
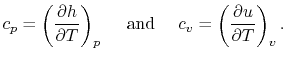
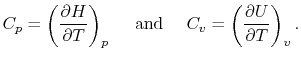
![]() depends
only on
depends
only on ![]() ,
,
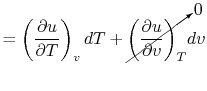
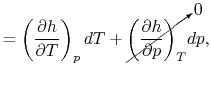
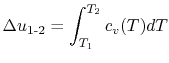
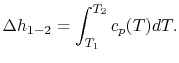
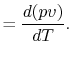
![]() and
and ![]() , and
, and ![]() vary with the
temperature, the variation being different for each gas. The general
trend is that heavy molecular weight gases (i.e., more complex gas
molecules than those listed in 2 or 3), have values of
vary with the
temperature, the variation being different for each gas. The general
trend is that heavy molecular weight gases (i.e., more complex gas
molecules than those listed in 2 or 3), have values of ![]() closer to unity than diatomic gases, which, as can be seen above,
are closer to unity than monatomic gases. For example, values of
closer to unity than diatomic gases, which, as can be seen above,
are closer to unity than monatomic gases. For example, values of
![]() below 1.2 are typical of Freons which have molecular
weights of over one hundred.2.3
below 1.2 are typical of Freons which have molecular
weights of over one hundred.2.3
![]() and
and ![]() depend on pressure as well as on temperature, and the above
relations will not all apply. In this respect, the ideal gas is a
very special model.
depend on pressure as well as on temperature, and the above
relations will not all apply. In this respect, the ideal gas is a
very special model.
![]() ,
,
![]() , and
, and
![]() ,
,
![]() or
or ![]() in the above result using the ideal
gas law, or carry out the derivation slightly differently, to also
show that
in the above result using the ideal
gas law, or carry out the derivation slightly differently, to also
show that