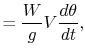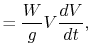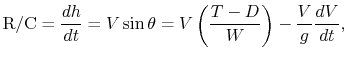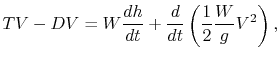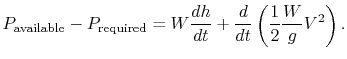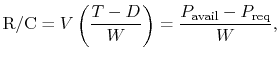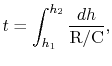13.5 Climbing Flight
Any excess in power beyond that required to overcome drag will cause
the vehicle increase kinetic or potential energy. We consider this
case by resolving forces about the direction of flight,
Figure 13.6, and equating these with
accelerations.
Figure 13.6:
Force balance for an aircraft in climbing flight.
|
|
where
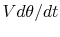 is the acceleration normal to the flight path
and
is the acceleration normal to the flight path
and 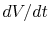 is the acceleration tangent to the flight path. So the
change in height of the vehicle (the rate of climb,
is the acceleration tangent to the flight path. So the
change in height of the vehicle (the rate of climb,
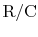 ) is
) is
which is instructive to rewrite in the form
or
In words:
For steady climbing flight,
and the time-to-climb is
where
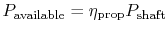 , for example, and
, for example, and
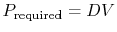 .
The power available is a function of the propulsion system, the
flight velocity, altitude, etc. Typically it takes a form such as
that shown in Figure 13.7. The shortest
time-to-climb occurs at the flight velocity where
.
The power available is a function of the propulsion system, the
flight velocity, altitude, etc. Typically it takes a form such as
that shown in Figure 13.7. The shortest
time-to-climb occurs at the flight velocity where
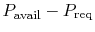 is a maximum. We conclude
this section with a dramatic photograph of an F-16 in a vertical,
accelerated climb, Figure 13.8.
is a maximum. We conclude
this section with a dramatic photograph of an F-16 in a vertical,
accelerated climb, Figure 13.8.
Figure 13.7:
Typical behavior of power available as a function of
flight velocity.
|
|
Figure 13.8:
Lockheed Martin F-16 performing a vertical accelerated
climb.
|
|
UnifiedTP
|