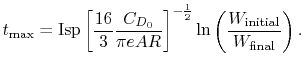13.4 Aircraft Endurance
If the time spent in the air is of interest and not the distance
traveled then one is concerned with endurance. The maximum endurance
of an aircraft (or the time aloft) refers to a flight condition that
requires the minimum fuel power. Assuming that the overall propulsion
system efficiency,
 , defined as the propulsive power
over the fuel
power, is constant, maximum endurance can be obtained by minimizing
the required propulsive power or rate of energy expenditure,
, defined as the propulsive power
over the fuel
power, is constant, maximum endurance can be obtained by minimizing
the required propulsive power or rate of energy expenditure, 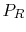 , as
shown in Figure 13.3.
, as
shown in Figure 13.3.
We can determine the aerodynamic configuration which provides the
minimum energy expenditure:
so
where
Then
So the minimum power required (maximum endurance) occurs when
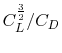 is a maximum. With a little algebra we can
arrive at an expression for the maximum endurance. Setting
is a maximum. With a little algebra we can
arrive at an expression for the maximum endurance. Setting
we find that
and
Thus the minimum power (maximum endurance) condition occurs at a
speed which is
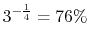 of the minimum drag
(maximum range) condition. The corresponding lift-to-drag ratio is
86.6% of the maximum lift-to-drag ratio, shown in
Figure 13.5.
of the minimum drag
(maximum range) condition. The corresponding lift-to-drag ratio is
86.6% of the maximum lift-to-drag ratio, shown in
Figure 13.5.
Figure 13.5:
Relationship between condition for maximum endurance and
maximum range.
|
|
Continuing
which can be substituted into
Such that, for maximum endurance,
which can be integrated (assuming constant Isp) to yield
UnifiedTP
|


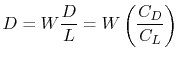
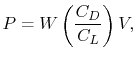
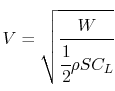
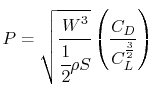
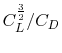 is a maximum. With a little algebra we can
arrive at an expression for the maximum endurance. Setting
is a maximum. With a little algebra we can
arrive at an expression for the maximum endurance. Setting
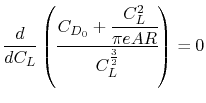
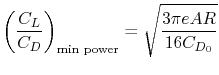
![$\displaystyle V_{\textrm{min power}} = \sqrt{\cfrac{W}{\cfrac{1}{2}\rho S C_{L,...
...}{\rho^2}\frac{1}{C_{D_0}}\left(\frac{1}{\pi e AR}\right)\right]^{\frac{1}{4}}.$](img1635.png)
![$\displaystyle D_{\textrm{minimum power}} = W\left[\frac{16}{3}\frac{C_{D_0}}{\pi e AR}\right]^{\frac{1}{2}},$](img1637.png)
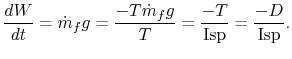
![$\displaystyle \frac{dW}{dt} = \frac{-W}{\textrm{Isp}}\left[\frac{16}{3}\frac{C_{D_0}}{\pi e AR}\right]^{\frac{1}{2}},$](img1639.png)