

|
|
| Thermodynamics and Propulsion | |
18.6 Muddiest Points on Chapter 18
MP 18..1
For an electric heated strip embedded between two layers,
what would the temperature distribution be if the two side
temperatures were not equal?
If the two temperatures on the outer surfaces of the composite layer
were
MP 18..2
Why did you change the variable and write the derivative
The heat balance and derivation of the equation for temperature Equation (18.8) is given in Section 18.2 of the notes. This is
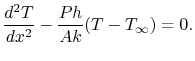
It is not necessary to change variables, and one could solve (18.8) as is or in the form
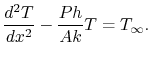
However, since: (1) the reference temperature is
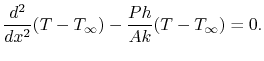
MP 18..3
What types of devices use heat transfer fins?
A number of types of heat exchangers use fins. Examples of the use of fins you may have seen are cooling fins on motorcycle engine heads, cooling fins on electric power transformers, or cooling fins on air conditioners.
MP 18..4
Why did the Stegosaurus have cooling fins? Could the
stegosaurus have ``heating fins?''
My knowledge of this issue extends only to reading about it in the text by Lienhard (see reference in notes). The journal article referenced in that text is: Farlow, J. O., Thompson, C. V., and Rosner, D.E., ``Plates of the Dinosaur Stegosaurus: Forced Convection Heat Loss Fins?'', Science, vol. 192, no. 4244, 1976, pp. 1123-1125 and cover.
MP 18..5
In equation
MP 18..6
In the lumped parameter transient heat transfer problem,
does a high density ``slow down'' heat transfer?
It doesn't. The high density slows down the rate at which the object changes temperature; high density means more ``heat capacity.'' UnifiedTP |