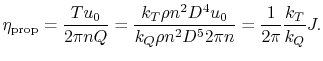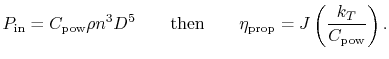Subsections
11.7 Performance of Propellers
In this section we will examine propeller engines. Examples of
propeller-powered vehicles are shown in
Figures 11.22 and 11.23.
Figure 11.22:
Cessna Skyhawk single engine propeller
plane (Cessna, 2000)
|
|
Figure 11.23:
The V-22 Osprey utilizes tiltrotor
technology (Boeing, 2000)
|
|
Each propeller blade is a rotating airfoil which produces lift and
drag, and because of a (complex helical) trailing vortex system has
an induced upwash and an induced downwash.
Figure 11.24 shows a schematic of a propeller.
Figure 11.24:
Schematic of propeller (McCormick, 1979)
|
|
The two quantities of interest are the thrust ( )11.1 and the torque
(
)11.1 and the torque
(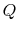 ). We can write expressions for these for a small radial element
(
). We can write expressions for these for a small radial element
(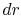 ) on one of the blades:
) on one of the blades:
where
and
It is possible to integrate the relationships as a function of 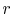 with the appropriate lift and drag coefficients for the local
airfoil shape, but determining the induced upwash (
with the appropriate lift and drag coefficients for the local
airfoil shape, but determining the induced upwash (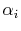 ) is
difficult because of the complex helical nature of the trailing
vortex system. In order to learn about the details of propeller
design, it is necessary to do this. However, for our purposes, we
can learn about the overall performance features using the integral
momentum theorem, some further approximations called ``actuator disk
theory,'' and dimensional analysis.
) is
difficult because of the complex helical nature of the trailing
vortex system. In order to learn about the details of propeller
design, it is necessary to do this. However, for our purposes, we
can learn about the overall performance features using the integral
momentum theorem, some further approximations called ``actuator disk
theory,'' and dimensional analysis.
Figure 11.25:
Control volume for analysis of a propeller (McCormick,
1979)
|
|
The control volume shown in Figure 11.25 has
been drawn far enough from the device so that the pressure is
everywhere equal to a constant. This is not required, but it makes
it more convenient to apply the integral momentum theorem. We will
also assume that the flow outside of the propeller streamtube does
not have any change in total pressure. Then since the flow is steady
we apply:
Since the pressure forces everywhere are balanced, then the only
force on the control volume is due to the change in momentum flux
across its boundaries. Thus by inspection, we can say that
We can arrive at the same result in a step-by-step manner as we did
for the jet engine example previously:
Note that the last term is identically equal to zero by conservation
of mass. If the mass flow in and out of the propeller streamtube are
the same (as we have defined), then the net mass flux into the rest
of the control volume must also be zero.
So we have:
as we reasoned before. The power expended is equal to the power
imparted to the fluid which is the change in kinetic energy of the
flow as it passes through the propeller,
The propulsive power - the rate at which useful work is done - is
the thrust multiplied by the flight velocity:
The propulsive efficiency is then the ratio of these two:
This is the same expression as we arrived at before for the jet
engine (as you might have expected).
11.7.3 Actuator Disk Theory
To understand more about the performance of propellers, and to
relate this performance to simple design parameters, we will apply
actuator disk theory. We model the flow through the propeller as
shown in Figure 11.26 and make the following
assumptions:
- Neglect rotation imparted to the flow.
- Assume the Mach number is
low so that the flow behaves as an incompressible fluid.
- Assume
the flow outside the propeller streamtube has constant stagnation
pressure (no work is imparted to it).
- Assume that the flow is
steady. Smear out the moving blades so they are one thin steady disk
that has approximately the same effect on the flow as the moving
blades (the ``actuator disk'').
- Across the actuator disk, assume
that the pressure changes discontinuously, but the velocity varies
in a continuous manner.
Figure 11.26:
Schematic of actuator disk model (Kerrebrock).
|
|
We then take a control volume around the disk as shown in
Figure 11.27.
Figure 11.27:
Control volume around actuator disk.
|
|
The force,  , on the disk is
, on the disk is
so the power is
We also know that the power is
Thus we see that the velocity at the disk is
Half of the axial velocity change occurs upstream of the disk and
half occurs downstream of the disk.
We can now find the pressure upstream and downstream of the disk by
applying the Bernoulli equation in the regions of the flow where the
pressure and velocity are varying continuously:
from which we can determine
We generally don't measure or control
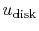 directly.
Therefore, it is more useful to write our expressions in terms of
flight velocity
directly.
Therefore, it is more useful to write our expressions in terms of
flight velocity 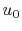 , thrust,
, thrust,  , (which must equal drag for
steady level flight) and propeller disk area,
, (which must equal drag for
steady level flight) and propeller disk area,
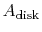 .
.
so
from which we can obtain an expression for the exit velocity in
terms of thrust and flight velocity, which are vehicle parameters:
The other parameters of interest become
and
This is the ideal (minimum) power required to drive the
propeller. In general, the actual power required would be about
15% greater than this. Lastly, the propulsive efficiency is
There are several important trends that are apparent upon
consideration of these equations. We see that the propulsive
efficiency is zero when the flight velocity is zero (no useful work,
just a force), and tends towards one when the flight velocity
increases. In practice, the propulsive efficiency typically peaks at
a level of around 0.8 for a propeller before various aerodynamic
effects act to decay its performance as will be shown in the
following section.
11.7.4 Dimensional Analysis
We will now use dimensional analysis to arrive at a few important
parameters for the design and choice of a propeller. Dimensional
analysis leads to a number of coefficients which are useful for
presenting performance data for propellers.
Table 11.2:
Propeller Parameters and their Units
| Parameter |
Symbol |
Units |
| propeller diameter |
D |
m |
| propeller speed |
n |
rev/s |
| torque |
Q |
Nm |
| thrust |
T |
N |
| fluid density |
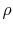
|
kg/m3 |
| fluid viscosity |
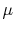
|
m2/s |
| fluid bulk elasticity modulus |
K |
N/m2 |
| flight velocity |
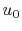
|
m/s |
11.7.4.1 Thrust Coefficient
Then putting this in dimensional form
where 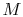 is a unit of mass,
is a unit of mass, 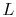 is a unit of length, and here
is a unit of length, and here  is a unit of time. Dimensional consistency requires
is a unit of time. Dimensional consistency requires
So
We can now consider the three terms in the square brackets.
This last coefficient is typically called the advance ratio
and given the symbol 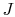 . Thus we see that the thrust may be written
as
. Thus we see that the thrust may be written
as
which is often expressed as
where 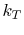 is called the thrust coefficient and in general is a
function of propeller design, Re,
is called the thrust coefficient and in general is a
function of propeller design, Re,
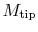 and
and 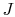 .
.
11.7.4.2 Torque Coefficient
We can follow the same steps to arrive at a relevant expression and
functional dependence for the torque or apply physical reasoning.
Since torque is a force multiplied by a length, it follows that
where 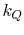 is called the torque coefficient and in general is a
function of propeller design, Re,
is called the torque coefficient and in general is a
function of propeller design, Re,
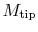 , and
, and 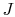 .
.
11.7.4.3 Efficiency
The power supplied to the propeller is
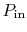 where
where
The useful power output is
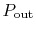 where
where
Therefore the efficiency is given by
11.7.4.4 Power Coefficient
The power required to drive the propeller is
which is often written using a power coefficient
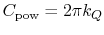 ,
,
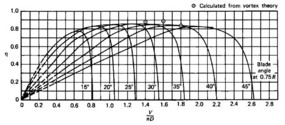
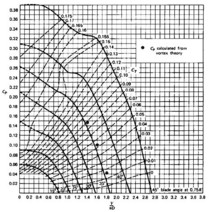
Typical propeller performance curves are shown in
Figures 11.28, 11.29, and
11.30.
Figure 11.28:
Typical propeller
efficiency curves as a function of advance ratio (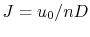 ) and
blade angle (McCormick, 1979).
) and
blade angle (McCormick, 1979).
|
|
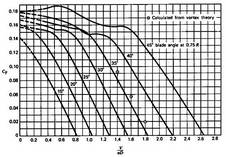
Figure 11.29:
Typical propeller thrust
curves as a function of advance ratio (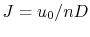 ) and blade angle
(McCormick, 1979).
) and blade angle
(McCormick, 1979).
|
|
Figure 11.30:
Typical propeller power
curves as a function of advance ratio (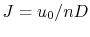 ) and blade angle
(McCormick, 1979).
) and blade angle
(McCormick, 1979).
|
|
UnifiedTP
|


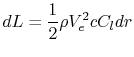
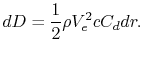
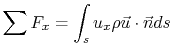
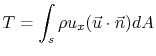
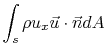
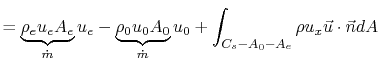
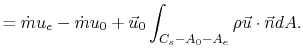

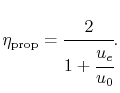
![]() , on the disk is
, on the disk is
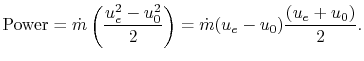
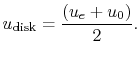
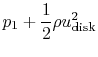
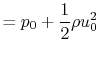
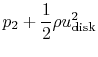
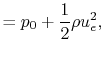
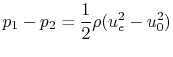
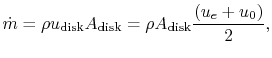
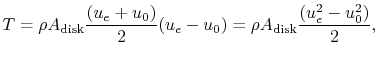
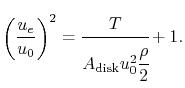
![$\displaystyle \frac{u_{\textrm{disk}}}{u_0} = \frac{1}{2}\left[\cfrac{T}{A_{\textrm{disk}}u_0^2\cfrac{\rho}{2}}+1\right]^{\frac{1}{2}}+\frac{1}{2}$](img1475.png)
![$\displaystyle \textrm{Power} = T u_{\textrm{disk}} = \frac{1}{2} T u_0\left[\le...
...frac{T}{A_{\textrm{disk}}u_0^2\cfrac{\rho}{2}}+1\right)^{\frac{1}{2}}+1\right].$](img1476.png)
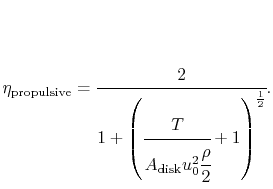
![$\displaystyle = \textrm{constant}\times \rho n^2 D^4 \times\textrm{function of}...
...^d;\left(\frac{K}{\rho D^2 n^2}\right)^e;\left(\frac{u_0}{D n}\right)^f\right].$](img1497.png)
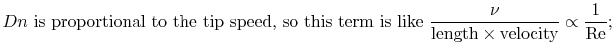
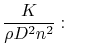
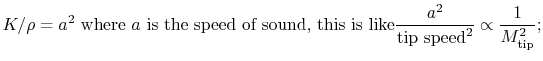
![]() where
where