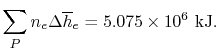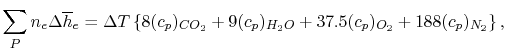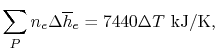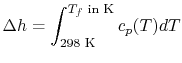Subsections
15.5 Adiabatic Flame Temperature
For a combustion process that takes place adiabatically with no
shaft work, the temperature of the products is referred to as the
adiabatic flame temperature. This is the maximum temperature that
can be achieved for given reactants. Heat transfer, incomplete
combustion, and dissociation all result in lower temperature. The
maximum adiabatic flame temperature for a given fuel and oxidizer
combination occurs with a stoichiometric mixture (correct
proportions such that all fuel and all oxidizer are consumed). The
amount of excess air can be tailored as part of the design to
control the adiabatic flame temperature. The considerable distance
between present temperatures in a gas turbine engine and the maximum
adiabatic flame temperature at stoichiometric conditions is shown in
Figure 3.24(b), based on a compressor exit temperature
of
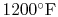 (922 K).
(922 K).
Figure 15.3:
Schematic of adiabatic
flame temperature
|
|
An initial view of the concept of adiabatic flame temperature is
provided by examining two reacting gases, at a given pressure, and
asking what the end temperature is. The process is shown
schematically in Figure 15.3, where
temperature is plotted versus the percentage completion of the
reaction. The initial state is 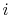 and the final state is
and the final state is 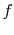 , with
the final state at a higher temperature than the initial state. The
solid line in the figure shows a representation of the ``actual''
process.
, with
the final state at a higher temperature than the initial state. The
solid line in the figure shows a representation of the ``actual''
process.
To see how we would arrive at the final completion state the dashed
lines break the state of reaction change into two parts. Process (1)
is reaction at constant 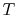 and
and 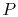 . To carry out such a process, we
would need to extract heat. Suppose the total amount of heat
extracted per unit mass is
. To carry out such a process, we
would need to extract heat. Suppose the total amount of heat
extracted per unit mass is 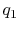 . The relation between the enthalpy
changes in Process (1) is
. The relation between the enthalpy
changes in Process (1) is
where 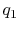 is the ``heat of reaction.''
is the ``heat of reaction.''
For Process (2), we put this amount back into the products to raise
their temperature to the final level. For this process,
or, if we can approximate the specific heat as constant (using some
appropriate average value)
For the overall process there is no work done and no heat exchanged
so that the difference in enthalpy between initial and final states
is zero:
The temperature change during this second process is therefore given
by (approximately)
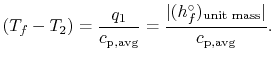 |
(15..5) |
The value of the adiabatic flame temperature given in
Equation (15.5) is for 100%
completion of the reaction. In reality, as the temperature
increases, the tendency is for the degree of reaction to be less
than 100%. For example, for the combustion of hydrogen and oxygen,
at high temperatures the combustion product (water) dissociates back
into the simpler elemental reactants. The degree of reaction is thus
itself a function of temperature that needs to be computed. We used
this idea in discussing the stoichiometric ramjet, when we said that
the maximum temperature was independent of flight Mach number and
hence of inlet stagnation temperature. It is also to be emphasized
that the idea of a constant (average) specific heat,
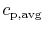 , is for illustration and not inherently part of
the definition of adiabatic flame temperature.
, is for illustration and not inherently part of
the definition of adiabatic flame temperature.
An example computation of adiabatic flame temperature is furnished
by the combustion of liquid octane at
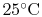 with
400% theoretical air. The reaction is
with
400% theoretical air. The reaction is
For an adiabatic process
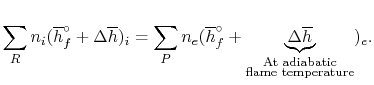 |
(15..6) |
We can again think of the general process in steps:
- Bring reactants to
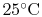 [the term
[the term
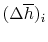 ] from the initial
temperature, using whatever heat transfer,
] from the initial
temperature, using whatever heat transfer, 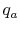 , is needed. In this
example we do not need step (i) because we are already at the
reference temperature.
, is needed. In this
example we do not need step (i) because we are already at the
reference temperature.
- Reaction at
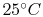 [the term
[the term
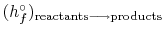 ]. There will be some
heat transfer in this step,
]. There will be some
heat transfer in this step, 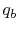 , out of the combustor.
, out of the combustor.
- Put back heat
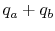 into the products of combustion.
The resulting temperature is the adiabatic flame temperature.
into the products of combustion.
The resulting temperature is the adiabatic flame temperature.
In the present case Equation (15.6)
is, explicitly:
We can examine the terms in the
SFEE separately, starting with the heat of formation terms, and
keeping track of units:
The exit state at the adiabatic flame temperature is specified by:
We find the adiabatic flame temperature in three ways:
- an approximate solution using an average value of
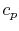 ,
,
- a more accurate one using the tabulated evolution of
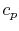 with temperature,
with temperature,
- or a more accurate solution using the tabulated values for gas enthalpy in
Table A.8 of SB&VW.
From Figure 15.2 we can use the
values at 500 K as representative. These are:
| Gas |
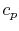 (kJ/kmole)
(kJ/kmole) |
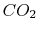
|
45 |
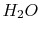
|
35 |
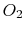
|
30 |
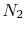
|
30 |
Using
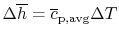 ,
,
where
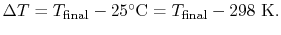
and using the exit state calculated above, find that
Tables give the following evolutions of specific heats with
temperature:
| Gas |
Evolution of
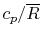 with
with 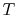 (kJ/kmol)
(kJ/kmol) |
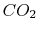
|
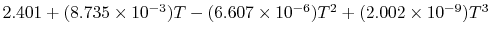
|
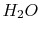
|
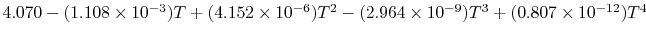
|
|
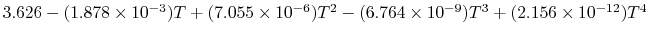
|
|
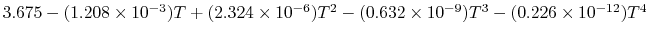
|
Using
and the same equation as above, we obtain
| |
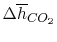
|
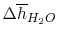
|
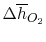
|
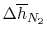
|
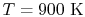
|
28,041 |
21,924 |
19,246 |
18,221
kJ/kmole |
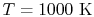
|
33,405 |
25,978 |
22,707 |
21,460
kJ/kmole |
Plugging in the numbers shows the answer is between these two
conditions. Linearly interpolating gives a value of
Muddy Points
Does ``adiabatic flame temperature'' assume 100% combustion?
(MP 15.7)
What part of the computation for adiabatic flame temperature
involves iteration? (MP 15.8)
UnifiedTP
|