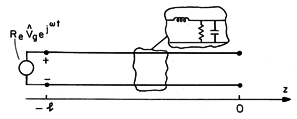
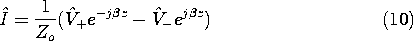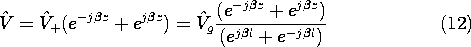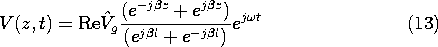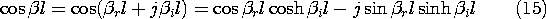The distributed parameter transmission line of Sec. 14.1 is now generalized to include certain types of dissipation by using the incremental circuit shown in Fig. 14.7.1 . The capacitance per unit length C is shunted by a conductance per unit length G and in series with the inductance per unit length L is the resistance per unit length R.
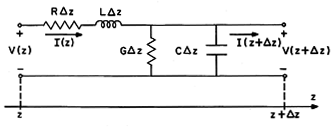
If the line really were made up of so many lumped parameter elements that it could be described by continuum equations, G would be the conductance per unit length of the lossy capacitors (Sec. 7.9) and R would be the resistance per unit length of the inductors. More often, G and R (like L and C) are either equivalent to or a model of a physical system. Examples are discussed in the next two sections.
The steps leading to the generalized transmission line equations
are suggested by Eqs. 14.1.1 through 14.1.5. In requiring that the
currents at the terminal on the right sum to zero, there is now an
additional current through the shunt conductance. In the limit where
 z
z  0,
0,

Similarly, in summing the voltages around the loop, there is now a
voltage drop across the series resistance. Again, in the limit  z
z
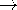 0,
0,

As should be expected, with the introduction of dissipation represented by G and R, V(z, t) and I(z, t) no longer take the form of waves propagating without distortion. That is, substitution shows that solutions no longer take the form of (14.4.1)-(14.4.3). As a result, we would have to work considerably harder than in Secs. 14.3-14.4 to describe transients on lossy transmission lines. However, although somewhat more involved then before, the sinusoidal steady state response follows from the approach illustrated in Secs. 14.5-14.6.
With the objective of describing the sinusoidal steady state, complex amplitude representations of V and I (14.5.2) are substituted into (1) and (2) to give


To obtain an expression for the voltage alone, (3) is substituted into the derivative of (4).
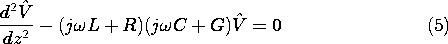
With the voltage found from this equation, the current follows from (4).

Albeit complex, the coefficient in (5) is constant, so it is again appropriate to look for exponential solutions. Using the convention established in Sec. 14.5, we look for solutions exp (-jkz). Substitution into (5) then shows that
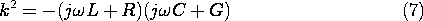
So as to be clear in distinguishing the two roots of this dispersion
equation, we define  as having a positive real part and
write the roots as
as having a positive real part and
write the roots as

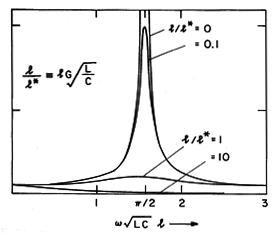
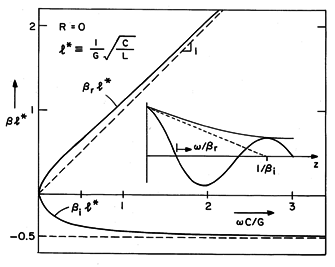
These roots, k = kr + jki, are pictured as a function of frequency
in Fig. 14.7.2. From (7), k2 is in the lower half-plane. It
follows that the value of k having a positive real part (defined as
 ) has a negative imaginary part.
) has a negative imaginary part.
 . The real and imaginary parts, respectively, of
the complex wave number
. The real and imaginary parts, respectively, of
the complex wave number  relate to the phase velocity and rate
of decay of the wave, as shown.
relate to the phase velocity and rate
of decay of the wave, as shown. These definitions take on physical significance when the solutions to (5) are written as

because it is then clear that we have defined  so that V+
represents a wave with points of constant phase propagating in the
+z direction. Note that because
so that V+
represents a wave with points of constant phase propagating in the
+z direction. Note that because  i is negative, this wave
decays in the +z direction, as shown in Fig. 14.7.2. Similarly,
i is negative, this wave
decays in the +z direction, as shown in Fig. 14.7.2. Similarly,
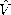 - is the complex amplitude at z = 0 of a wave that
decays in the -z direction and has phases propagating in the -z
direction.
- is the complex amplitude at z = 0 of a wave that
decays in the -z direction and has phases propagating in the -z
direction.


 , the current expression
follows from substituting (9) into (6)
, the current expression
follows from substituting (9) into (6)