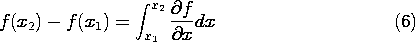2.2
Gauss' Integral Theorem

The operator that is required for (2.1.1) to hold has been identified by considering an incremental volume element. But does the relation hold for volumes of finite size?

The volume enclosed by the surface S can be subdivided into differential elements, as shown in Fig. 2.2.1. Each of the elements has a surface of its own with the i-th being enclosed by the surface S_i. We now prove that the surface integral of the vector A over the surface S is equal to the sum of the surface integrals over each surface S

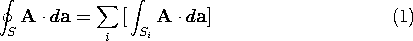
Note first that the surface normals of two surfaces between adjacent volume elements are oppositely directed, while the vector A has the same value for both surfaces. Thus, as illustrated in Fig. 2.2.1, the fluxes through surfaces separating two volume elements in the interior of S cancel.

Figure 2.2.1. (a) Three mutually perpendicular slices define an incremental volume in the volume V shown in cross-section. (b) Adjacent volume elements with common surface.

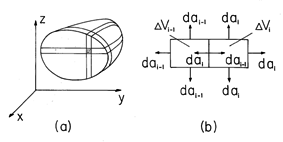
The only contributions to the summation in (1) which do not cancel are the fluxes through the surfaces which do not separate one volume element from another, i.e., those surfaces that lie on S. But because these surfaces together form S, (1) follows. Finally, with the right-hand side rewritten, (1) is

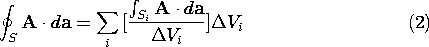
where V_i is the volume of the i-th element. Because these volume elements are differential, what is in brackets on the right in (2) can be represented using the definition of the divergence operator, (2.1.2).

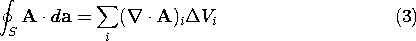
Gauss' integral theorem follows by replacing the summation over the differential volume elements by an integration over the volume.

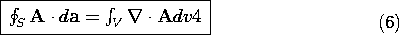
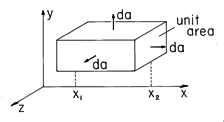
Example 2.2.1. One-Dimensional Theorem

If the vector A is one-dimensional so that

what does Gauss' integral theorem say about an integration over a volume V between the planes x = x₁ and x = x₂ and of unit cross-section in any y - z plane between these planes? The volume V and surface S are as shown in Fig. 2.2.2. Because A is x directed, the only contributions are from the right and left surfaces. These respectively have da = i_x dydz and da = -i_x dydz. Hence, substitution into (4) gives the familiar form,

which is a reminder of the one-dimensional analogy discussed in the introduction. Gauss' theorem extends into three dimensions the relationship that exists between the derivative and integral of a function.

Figure 2.2.2. Volume between planes x = x₁ and x = x₂ having unit area in y - z planes.