Of the five integral laws summarized in Table 1.8.1, three involve integrations over closed surfaces. By Gauss' theorem, (2.2.4), each of the surface integrals is now expressed as a volume integral. Because the volume is arbitrary, the integrands must vanish, and so the differential laws are obtained.
The differential form of Gauss' law follows from (1.3.1) in that table.
Magnetic flux continuity in differential form follows from (1.7.1).
In the integral charge conservation law, (1.5.2), there is a time derivative. Because the geometry of the integral we are considering is fixed, the time derivative can be taken inside the integral. That is, the spatial integration can be carried out after the time derivative has been taken. But becaus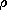e
is not only a function of t but of (x, y, z) as well, the time derivative is taken holding (x, y, z) constant. Thus, the differential charge conservation law is stated using a partial time derivative.
These three differential laws are summarized in Table 2.8.1.
