2.4
The Curl Operator

If the integral laws of Ampère and Faraday, (1.4.1) and (1.6.1), are to be written in terms of one type of integral, it is necessary to have an operator such that the contour integrals are converted to surface integrals. This operator is called the curl.

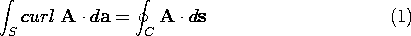
The operator is identified by making the surface an incremental one, a. At the particular point r where the operator is to be evaluated, pick a direction n and construct a plane normal to n through the point r. In this plane, choose a contour C around r that encloses the incremental area a. It follows from (1) that

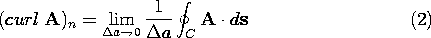
The shape of the contour C is arbitrary except that all its points are assumed to approach the point r under study in the limit a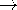 0. Such an arbitrary elemental surface with its unit normal n is illustrated in Fig. 2.4.1a. The definition of the curl operator given by (2) is independent of the coordinate system.

Figure 2.4.1. (a) Incremental contour for evaluation of the component of the curl in the direction of n. (b) Incremental contour for evaluation of x component of curl in Cartesian coordinates.

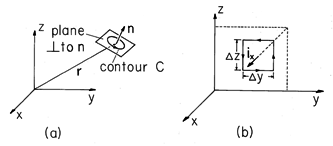
To express (2) in Cartesian coordinates, consider the incremental surface shown in Fig. 2.4.1b. The center of a is at the location (x,y,z), where the operator is to be evaluated. The contour is composed of straight segments at y y/2 and z z/2. To first order in y and z, it follows that the n = i_x component of (2) is

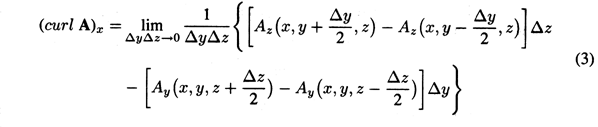
Here the first two terms represent integrations along the vertical segments, first in the +z direction and then in the -z direction. Note that integration on this second leg results in a minus sign, because there, A is oppositely directed to ds.

In the limit, (3) becomes

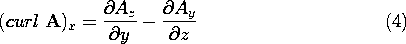
The same procedure, applied to elemental areas having normals in the y and z directions, result in three "components" for the curl operator.

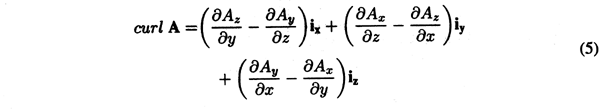
In fact, we should be able to select the surface for evaluating (2) as having a unit normal n in any arbitrary direction. For (5) to be a vector, its dot product with n must give the same result as obtained for the direct evaluation of (2). This is shown to be true in Appendix 2.

The result of cross-multiplying A by the del operator, defined by (2.1.6), is the curl operator. This is the reason for the alternate notation for the curl operator.

Thus, in Cartesian coordinates

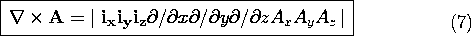
The problems give the opportunity to derive expressions having similar forms in cylindrical and spherical coordinates. The results are summarized in Table I at the end of the text.