In Sec. 2.4, curl A was identified as that vector function which had an integral over a surface S that could be reduced to an integral on A over the enclosing contour C. This was done by applying (2.4.1) to an incremental surface. But does this relation hold for S and C of finite size and arbitrary shape?
The generalization to an arbitrary surface begins by subdividing S into differential area elements, each enclosed by a contour C . As shown in Fig. 2.5.1, each differential contour coincides in direction with the positive sense of the original contour. We shall now prove that
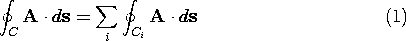
where the sum is over all contours bounding the surface elements into which the surface S has been subdivided.
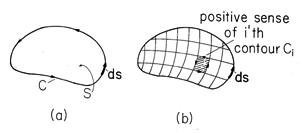
Figure 2.5.1. Arbitrary surface enclosed by contour C is subdivided into incremental elements, each enclosed by a contour having the same sense as C. Because the segments are followed in opposite senses when evaluated for the adjacent area elements, line integrals along those segments of the contours which separate two adjacent surface elements add to zero in the sum of (1). Only those line integrals remain which pertain to the segments coinciding with the original contour. Hence, (1) is demonstrated.
Next, (1) is written in the slightly different form.
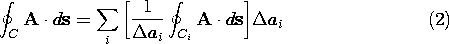
We can now appeal to the definition of the component of the curl in the direction of the normal to the surface element, (2.4.2), and replace the summation by an integration.
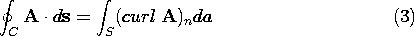
Another way of writing this expression is to take advantage of the vector character of the curl and the definition of a vector area element, da = n da :
This is Stokes' integral theorem. If a vector function can be written as the curl of a vector A, then the integral of that function over a surface S can be reduced to an integral of A on the enclosing contour C.
