With the help of Stokes' theorem, Ampère's integral law (1.4.1) can now be stated as
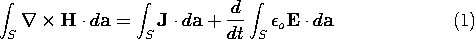
That is, by virtue of (2.5.4), the contour integral in (1.4.1) is replaced by a surface integral. The surface S is fixed in time, so the time derivative in (1) can be taken inside the integral. Because S is also arbitrary, the integrands in (1) must balance.
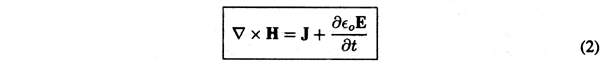
This is the differential form of Ampère's law. In the last term, which is called the displacement current density, a partial time derivative is used to make it clear that the location (x, y, z) at which the expression is evaluated is held fixed as the time derivative is taken.
In Sec. 1.5, it was seen that the integral forms of Ampère's and
Gauss' laws combined to give the integral form of the charge
conservation law. Thus, we should expect that the differential forms
of these laws would also combine to give the differential charge
conservation law. To see this, we need the identity 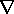
 (
(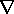 x A) = 0 (Problem 2.4.5). Thus, the divergence of
(2) gives
x A) = 0 (Problem 2.4.5). Thus, the divergence of
(2) gives
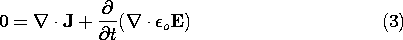
Here the time and space derivatives have been interchanged in the last term. By Gauss' differential law, (2.3.1), the time derivative is of the charge density, and so (3) becomes the differential form of charge conservation, (2.3.3). Note that we are taking a differential view of the interrelation between laws that parallels the integral developments of Sec. 1.5.
Finally, Stokes' theorem converts Faraday's integral law (1.6.1) to integrations over S only. It follows that the differential form of Faraday's law is

The differential forms of Maxwell's equations in free space are summarized in Table 2.8.1.

