In the presence of materials, fields vary in space over at least two length scales. The microscopic scale is typically the distance between atoms or molecules while the much larger macroscopic scale is typically the dimension of an object made from the material. As developed in the previous chapter, fields in polarized media are averages over the microscopic scale of the dipoles. In effect, the experimental determination of the polarization constitutive law relating the macroscopic P and E (Sec. 6.4) does not deal with the microscopic field.
With the understanding that experimentally measured values will again be used to evaluate macroscopic parameters, we assume that the average force acting on an unpaired or free charge, q, within matter is of the same form as the Lorentz force, (1.1.1).

By contrast with a polarization charge, a free charge is not bound to the atoms and molecules, of which matter is constituted, but under the influence of the electric and magnetic fields can travel over distances that are large compared to interatomic or intermolecular distances. In general, the charged particles collide with the atomic or molecular constituents, and so the force given by (1) does not lead to uniform acceleration, as it would for a charged particle in free space. In fact, in the conventional conduction process, a particle experiences so many collisions on time scales of interest that the average velocity it acquires is quite low. This phenomenon gives rise to two consequences. First, inertial effects can be disregarded in the time average balance of forces on the particle. Second, the velocity is so low that the forces due to magnetic fields are usually negligible. (The magnetic force term leads to the Hall effect, which is small and very difficult to observe in metallic conductors, but because of the relatively larger translational velocities reached by the charge carriers in semiconductors, more easily observed in these.)
With the driving force ascribed solely to the electric field and counterbalanced by a "viscous" force, proportional to the average translational velocity v of the charged particle, the force equation becomes

where the upper and lower signs correspond to particles of positive
and negative charge, respectively. The coefficients 
 are positive
constants representing the time average "drag" resulting from
collisions of the carriers with the fixed atoms or molecules through
which they move.
are positive
constants representing the time average "drag" resulting from
collisions of the carriers with the fixed atoms or molecules through
which they move.
Written in terms of the mobilities, 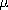
 ,
the velocities of the positive and negative particles follow from
(2) as
,
the velocities of the positive and negative particles follow from
(2) as

where 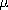
 = |q
= |q |/
|/
 .
The mobility is defined as positive. The positive and negative
particles move with and against the electric field intensity,
respectively.
.
The mobility is defined as positive. The positive and negative
particles move with and against the electric field intensity,
respectively.
Now suppose that there are two types of charged particles, one positive and the other negative. These might be the positive sodium and negative chlorine ions resulting when salt is dissolved in water. In a metal, the positive charges represent the (zero mobility) atomic sites, while the negative particles are electrons. Then, with N+ and N-, respectively, defined as the number of these charged particles per unit volume, the current density is
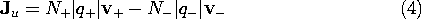
A flux of negative particles comprises an electrical current that is in a direction opposite to that of the particle motion. Thus, the second term in (4) appears with a negative sign. The velocities in this expression are related to E by (3), so it follows that the current density is
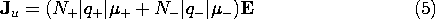
In terms of the same variables, the unpaired charge density is

Ohmic Conduction
In general, the distributions of particle densities N+ and N-
are determined by the electric field. However, in many materials, the
quantity in brackets in (5) is a property of the material, called
the electrical conductivity  .
.
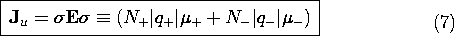
The MKS units of  are (ohm - m)-1 \equiv Siemens/m =
S/m.
are (ohm - m)-1 \equiv Siemens/m =
S/m.
In these materials, the charge densities N+ q+ and N- q-
keep each other in (approximate) balance so that there is little
effect of the applied field on their sum. Thus, the conductivity
 (r) is specified as a function of position in nonuniform
media by the distribution N
(r) is specified as a function of position in nonuniform
media by the distribution N in the material and by the local
mobilities, which can also be functions of r.
in the material and by the local
mobilities, which can also be functions of r.
The conduction constitutive law given by (7) is Ohm's law generalized in a field-theoretical sense. Values of the conductivity for some common materials are given in Table 7.1.1. It is important to keep in mind that any constitutive law is of restricted use, and Ohm's law is no exception. For metals and semiconductors, it is usually a good model on a sufficiently large scale. It is also widely used in dealing with electrolytes. However, as materials become semi-insulators, it can be of questionable validity.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Unipolar Conduction
To form an appreciation for the implications of Ohm's law, it will be helpful to contrast it with the law for unipolar conduction. In that case, charged particles of only one sign move in a neutral background, so that the expressions for the current density and charge density that replace (5) and (6) are


where the charge density  now carries its own sign. Typical of
situations described by these relations is the passage of ions through
air.
now carries its own sign. Typical of
situations described by these relations is the passage of ions through
air.
Note that a current density exists in unipolar conduction only if
there is a net charge density. By contrast, for Ohmic conduction,
where the current density and the charge density are given by (7)
and (6), respectively, there can be a current density at a location where
there is no net charge density. For example, in a metal, negative
electrons move through a background of fixed positively charged atoms.
Thus, in (7),  + = 0 and the conductivity is due solely to the
electrons. But it follows from (6) that the positive charges do have
an important effect, in that they can nullify the charge density of
the electrons. We will often find that in an Ohmic conductor there is
a current density where there is no net unpaired charge density.
+ = 0 and the conductivity is due solely to the
electrons. But it follows from (6) that the positive charges do have
an important effect, in that they can nullify the charge density of
the electrons. We will often find that in an Ohmic conductor there is
a current density where there is no net unpaired charge density.

