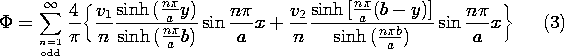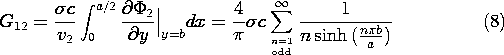7.4
Superposition and Uniqueness of Steady Conduction Solutions

The physical laws and boundary conditions are different, but the approach in this section is similar to that of Secs. 5.1 and 5.2 treating Poisson's equation.

In a material having the conductivity distribution (r) and source distribution s(r), a steady potential distribution must satisfy (7.2.4) with a source density -s on the right. Typically, the configurations of interest are as in Fig. 7.2.1, except that we now include the possibility of a distribution of current source density in the volume V. Electrodes are used to constrain this potential over some of the surface enclosing the volume V occupied by this material. This part of the surface, where the material contacts the electrodes, will be called S^'. We will assume here that on the remainder of the enclosing surface, denoted by S^", the normal current density is specified. Depicted in Fig. 7.2.1 is the special case where the boundary S^" is insulating and hence where the normal current density is zero. Thus, according to (7.2.1), (7.2.3), and (7.3.1), the desired E and J are found from a solution to

where

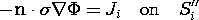
Except for the possibility that part of the boundary is a surface S^" where the normal current density rather than the potential is specified, the situation here is analogous to that in Sec. 5.1. The solution can be divided into a particular part [that satisfies the differential equation of (1) at each point in the volume, but not the boundary conditions] and a homogeneous part. The latter is then adjusted to make the sum of the two satisfy the boundary conditions.

Superposition to Satisfy Boundary Conditions

Suppose that a system is composed of a source-free conductor (s = 0) contacted by one reference electrode at ground potential and n electrodes, respectively, at the potentials v_j, j = 1, n. The contacting surfaces of these electrodes comprise the surface S^'. As shown in Fig. 7.2.1, there may be other parts of the surface enclosing the material that are insulating (J_i = 0) and denoted by S^". The solution can be represented as the sum of the potential distributions associated with each of the electrodes of specified potential while the others are grounded.

where

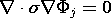
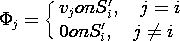
Each _j satisfies (1) with s = 0 and the boundary condition on S_i^" with J_i = 0. This decomposition of the solution is familiar from Sec. 5.1. However, the boundary condition on the insulating surface S^" requires a somewhat broadened view of what is meant by the respective terms in (2). As the following example illustrates, modes that have zero derivatives rather than zero amplitude at boundaries are now useful for satisfying the insulating boundary condition.

Example 7.4.1. Modal Solution with an Insulating Boundary

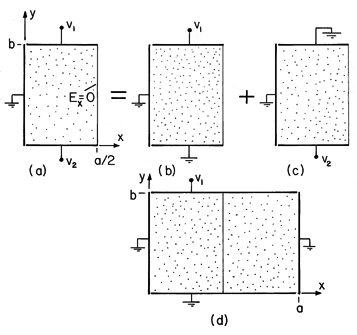
In the two-dimensional configuration of Fig. 7.4.1, a uniformly conducting material is grounded along its left edge, bounded by insulating material along its right edge, and driven by electrodes having the potentials v₁ and v₂ at the top and bottom, respectively.

Figure 7.4.1 (a) Two terminal pairs attached to conducting material having one wall at zero potential and another that is insulating. (b) Field solution is broken into part due to potential v₁ and (c) potential v₂. (d) The boundary condition at the insulating wall is satisfied by using the symmetry of an equivalent problem with all of the walls constrained in potential.

Decomposition of the potential, as called for by (2), amounts to the superposition of the potentials for the two problems of (b) and (c) in the figure. Note that for each of these, the normal derivative of the potential must be zero at the right boundary.

Pictured in part (d) of Fig. 7.4.1 is a configuration familiar from Sec. 5.5. The potential distribution for the configuration of Fig. 5.5.2, (5.5.9), is equally applicable to that of Fig. 7.4.1. This is so because the symmetry requires that there be no x-directed electric field along the surface x = a/2. In turn, the potential distribution for part (c) is readily determined from this one by replacing v₁ v₂ and y b - y. Thus, the total potential is

If we were to solve this problem without reference to Sec. 5.5, the modes used to expand the electrode potential would be zero at x = 0 and have zero derivative at the insulating boundary (at x = a/2).

The Conductance Matrix

With S_i^' defined as the surface over which the i-th electrode contacts the conducting material, the current emerging from that electrode is

[See Fig. 7.2.1 for definition of direction of da.] In terms of the potential decomposition represented by (2), this expression becomes

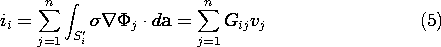
where the conductances are

Because _j is by definition proportional to v_j, these parameters are independent of the excitations. They depend only on the physical properties and geometry of the configuration.

Example 7.4.2. Two Terminal Pair Conductance Matrix

For the system of Fig. 7.4.1, (5) becomes

With the potential given by (3), the self-conductances G₁₁ and G₂₂ and the mutual conductances G₁₂ and G₂₁ follow by evaluation of (5). This potential is singular in the left-hand corners, so the self-conductances determined in this way are represented by a series that does not converge. However, the mutual conductances are determined by integrating the current density over an electrode that is at the same potential as the grounded wall, so they are well represented. For example, with c defined as the length of the conducting block in the z direction,

Uniqueness

With _i, J_i, (r), and s(r) given, a steady current distribution is uniquely specified by the differential equation and boundary conditions of (1). As in Sec. 5.2, a proof that a second solution must be the same as the first hinges on defining a difference potential _d = _a - _b and showing that, because _d = 0 on S^'_i and n _d = 0 on S_i^" in Fig. 7.2.1, _d must be zero.