6.02 Lab #4: Error Detection and Correction

Deadlines

Useful links

Goal

Implement the main building blocks of error detection and correction to handle bit errors. You will write the code for three components:

  1. Error detection using an Adler-32 checksum calculation.
  2. Error correction using a linear block code (rectangular parity).
  3. Error correction using a convolutional code with Viterbi decoding (both hard and soft decision decoding).
In addition to establishing the correctness of your software, you will compare the performance of the three error correction schemes (the rectangular parity code, Viterbi hard decoding, and Viterbi soft decision decoding for different parameters).

Instructions

See Lab #1 for a longer narrative about lab mechanics. The one-sentence version:

Complete the tasks below, submit your task files on-line before the deadline, and sign-up for your check-off interview with your TA.

As always, help is available in 32-083 (see the Lab Hours web page).

Task 1: Error Detection with the Adler-32 checksum (2 points)

The context for our error detection scheme is as follows. The sender sends a message to the receiver, protecting it with various error-correcting mechanisms (Tasks 2-4 below). These correction mechanisms reduce the bit-error rate (BER), but may not be able to eliminate all errors. So the receiver needs to know whether the message is correct or not, after it implements the decoding steps of the error correcting mechanisms. This error detection step is implemented by verifying the checksum of the message. If the checksum verifies correctly, the message is assumed to have been received correctly; otherwise, not.

Please consult the lecture notes for lecture 7 for details about various error detection schemes and how they are used. The description below focuses only on the essentials needed for the lab task at hand.

This task is to implement the Adler-32 checksum, a relatively recent invention (1995) that is also quite simple. It is now used in various popular compression libraries (notably zlib) and (in a sliding window form) in the rsync file synchronization utility. It works reasonably well for long messages (many tens of thousands of bits or more).

The Adler-32 checksum is computed as follows (see Lecture 7 if the description below isn't enough to do the task). The operations below work on 8-bit bytes of the message, interpreted as an unsigned integer. You can use lab4.bits_to_int(bit_sequence) to convert a sequence of 0/1 values into an unsigned integer value.

lab4_1.py is the template file for this task. 

# This is the template file for Lab #4, Task #1
import numpy
import lab4

# adler_checksum -- compute Adler32 checksum
# arguments:
#   bits -- numpy array of bits
# return value:
#   integer result
def adler_checksum(bits):
    pass # your code here

if __name__ == '__main__':
    if lab4.verify_checksum(adler_checksum):
        print "Task 1 succeeded on the test cases: congratulations!"

    # When ready for checkoff, enable the following line.
    lab4.checkoff(adler_checksum,task='L4_1')

Here's a description of the function you need to write:

result = adler_checksum(bits)
bits is numpy array of bits (0 and 1 values) for which the Adler-32 checksum is to be produced. Note that the length of bits is not guaranteed to be a multiple of 8. In that case, the last call to lab4.bits_to_int should be the trailing set of bits (which will be less than 8 in length). Return the 32-bit integer result.

lab4.verify_checksum tests your implementation with a few bit sequences. The table below gives the length in bits of two of the sequences and the expected values of A and B after all the bytes have been processed, but before the mod 65521 calculation. You may find this table useful in debugging. (In practice, you should be generating and writing such test cases on your own!)

SequenceLengthAB
#110215428
#28010314329

When you're ready to submit your code on-line, enable the call to lab4.checkoff. When submitting, run your task file using python602 because the submission sometimes does not work correctly when run from an integrated development environment.

Task 2: Single error correction with rectangular parity (3 points)

The goal of this task is to decode a rectangular parity block code, which can correct single errors, as discussed in Lecture 6. Once you decode a single block, decode a stream of bits composed of multiple blocks, each coded with rectangular parity.

lab4_2.py is the template file for this task. 

# This is the template file for Lab #4, Task #2
import numpy
import lab4

# compute even parity for a bit sequence
def even_parity(bits):
    return sum(bits) % 2

# rect_decode -- correct errors in a rectangular block code (an SEC code)
# arguments:
#   codeword -- numpy array of bits, whose length is equal to
#                     nrows*ncols + nrows + ncols
#               (order of bits in array: all the data bits,
#               row-by-row, followed by the row parity bits,
#               followed by the column parity bits).
#   nrows -- integer, number of rows in rectangular block
#   ncols -- integer, number of columns in rectangular block
# return value:
#   numpy array of size nrows*ncols of the most likely message bits
def rect_decode(codeword,nrows,ncols):
    # Your code here
    pass

# decode_stream -- decode a stream of blocks, each block encoded with 
# a rectangular parity code.  Each block has nrows*ncols + nrows + ncols
# bits when coded.  The nrows + ncols parity bits for each block are
# immeadiately following the block.
def decode_stream(stream,nrows,ncols):
    # Your code here
    pass

if __name__ == '__main__':
    # test your implementation
    #   first tests correct decode with no errors
    #   then tests correct decode with single error
    lab4.test_rect_decode(rect_decode)
    #   then test stream decoding ability (not exhaustively)
    lab4.test_stream_decode(decode_stream)
    
    # when ready for checkoff, enable the next line.
    #lab4.checkoff(rect_decode,decode_stream,task='L4_2')
You should write two functions:
block = rect_decode(codeword,nrows,ncols)
codeword is a numpy array of bits (0 and 1 values) with nrows*ncols data bits followed by nrows row parity bits and then ncols column parity bits, for a total of nrows*ncols + nrows + ncols bits. The function should check the row and column parity and correct any errors it determines. Please note that your code only needs to work for the cases of no errors and a single error. The function should return a numpy array containing the most likely message bits corresponding to the codeword.

Please use the function even_parity for parity checks; it will make your solution more readable.

decoded_message = decode_stream(stream, nrows, ncols)
stream is a numpy array of coded bits (0 or 1) obtained by taking an original message with m bits, breaking it up into blocks of nrows*ncols bits each, and then computing the rectangular parity for each block. The parity bits for each block are placed immediately after the block in the same order as described in the rect_decode function, above. The decode_stream function should make repeated calls to rect_decode.

lab4.test_rect_decode tests your implementation of rect_parity_decode, first with codewords containing no errors, then with codewords containing a single error. It reports any discrepencies it finds.

lab4.test_stream_decode tests your implementation of stream_decode and reports if the test succeeds or not.

When you're ready to submit your code on-line, enable the call to lab4.checkoff. When submitting, run your task file using python602 because the submission sometimes does not work correctly when run from an integrated development environment.

Task 3: Viterbi decoder for convolutional codes: Hard decision decoding (4 points)

As explained in Lecture 8, a convolutional encoder is characterized by two parameters: a constraint length K and a set of r generator functions {G0, G1, ...}. The encoder processes the message one bit at a time, generating a set of r parity bits {p0, p1, ...} by applying the generator functions to the current message bit, x[n], and K-1 of the previous message bits, x[n-1], x[n-2], ..., x[n-(K-1)]. The r parity bits are then transmitted and the encoder moves on to the next message bit.

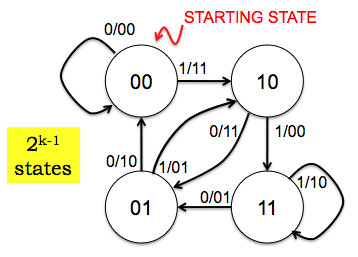
The operation of the encoder may be described as a state machine, as you know (we hope). The figure below is the state transition diagram for a rate 1/2 encoder with K=3 using the following two generator functions: 

G0: 111, i.e., p0[n] = (1*x[n] + 1*x[n-1] + 1*x[n-2]) mod 2
G1: 110, i.e., p1[n] = (1*x[n] + 1*x[n-1] + 0*x[n-2]) mod 2

A generator function can described compactly by simply listing its K coefficients as a K-bit binary sequence, or even more compactly (for a human reader) if we construe the K-bit sequence as an integer, e.g., G0: 7 and G1: 6. We will use the latter (integer) representation in this task.

In this diagram the states are labeled with the two previous message bits, x[n-1] and x[n-2], in left-to-right order. The arcs -- representing transitions between states as the encoder completes the processing of the current message bit -- are labeled with x[n]/p0p1.

You can read the transition diagram as follows: "If the encoder is currently in state 11 and if the current message bit is a 0, transmit the parity bits 01 and move to state 01 before processing the next message bit." And so on, for each combination of current states and message bits. The encoder starts in state 00 and you should assume that all the bits before the start were 0.

A stream of parity bits corrupted by additive noise arrives at the receiver. Using the information in these parity bits, the decoder attempts to deduce the actual sequence of states traversed by the encoder and recover the transmitted message. Because of errors, the receiver cannot know exactly what that sequence of states was, but it can determine the most likely sequence using the Viterbi decoding algorithm.

The Viterbi decoder, described in Lecture 9, works by determining a path metric PM[s,n] for each state s and bit time n. Consider all possible encoder state sequences that cause the encoder to be in state s at time n. In hard decision decoding, the most-likely state sequence is the one that produced the parity bit sequence nearest in Hamming distance to the sequence of received parity bits. Each increment in Hamming distance corresponds to a bit error. PM[s,n] records this smallest Hamming distance for each state at the specified time.

The Viterbi algorithm computes PM[…,n] incrementally. Initially

PM[s,0] = 0 if s == starting_state else ∞

The decoding algorithm uses the first set of r parity bits to compute PM[…,1] from PM[…,0]. Then, it uses the next set of r parity bits to compute PM[…,2] from PM[…,1]. It continues in this fashion until it has processed all the received parity bits.

Here are the steps for computing PM[…,n] from PM[…,n-1] using the next set of r parity bits to be processed:

For each state s:

  1. Looking at the encoder's state transition diagram, determine the two predecessor states α and β, which have transition arcs that arrive at state s.

    Using the rate 1/2, K=3 encoder above, if s is 10 then, in no particular order, α = 00 and β = 01.

  2. For the state transition α→s determine the r parity bits that the encoder would have transmitted; call this r-bit sequence p_α. Similarly, for the state transition β→s determine the r parity bits the encoder would have transmitted; call this r-bit sequence p_β.

    Continuing the example from Step 1: p_α = 11 and p_β = 01.

  3. Call the next set of r received parity bits p_received. Compute the Hamming distance between p_α and p_received. This Hamming distance is a branch metric for the state transition α→s, so we'll label it BM_α. Similarly, compute the Hamming distance between p_β and p_received; we'll call it BM_β.

    Continuing the example from Step 2: assuming the received parity bits p_received = 00, then BM_α = hamming(11,00) = 2 and BM_β = hamming(01,00) = 1.

  4. Compute two trial path metrics that correspond to the two possible paths leading to state s: 

      PM_α = PM[α,n-1] + BM_α
PM_β = PM[β,n-1] + BM_β

    PM_α is the Hamming distance between the transmitted bits and the parity bits received so far, assuming that we arrive at state s via state α. Similarly, PM_β is the Hamming distance between the transmitted and parity bits received so far, assuming we arrive at state s via state β.

    Continuing the example from Step 3: assuming PM[α,n-1]=5 and PM[β,n-1]=3, then PM_α=7 and PM_β=4.

  5. Now compute PM[s,n] by picking the smaller of the two trial path metrics. Also record which state we chose to be the most-likely predecessor state for s: 

      if PM_α <= PM_β:
    PM[s,n] = PM_α
    Predecessor[s,n] = α
else
    PM[s,n] = PM_β
    Predecessor[s,n] = β

    Completing the example from step 4: PM[s,n]=4 and Predecessor[s,n]=β.

We can use the following recipe at the receiver to determine the transmitted message:

  1. Initialize PM[…,0] as described above.

  2. Use the Viterbi algorithm to compute PM[…,n] from PM[…,n-1] and the next r parity bits; repeat until all received parity bits have been consumed. Call the last time point N.

  3. Identify the most-likely ending state of the encoder by finding the state s that has the mimimum value of PM[s,N]. If there are several states with the same minimum value, choose one arbitrarily.

  4. Determine message bit that caused the transition to state s. You can make this determination simply from knowing s; you don't need to know the predecessor state. Set s=Predecessor[s,N], decrement N, and repeat this step as long as N > 0, accumulating the message bits in reverse order.

In this task we'll write the code for some methods of the ViterbiDecoder class. One can make an instance of the class, supplying K and the parity generator functions, and then use the instance to decode messages transmitted by the matching encoder.

The decoder will operate on a sequence of received voltage samples; the choice of which sample to digitize to determine the message bit has already been made, so there's one voltage sample for each bit. The transmitter has sent a 0 Volt sample for a "0" and a 1 Volt sample for a "1", but those nominal voltages have been corrupted by additive Gaussian noise zero mean and non-zero variance. Assume that 0's and 1's appear with equal probability in the transmitted message.

lab4_3.py is the template file for this task (not shown inline here).

You need to write the following functions:

number = branch_metric(self,expected,received)
expected is an r-element list of the expected parity bits (or you can also think of them as voltages given how we send bits down the channel). received is an r-element list of actual sampled voltages for the incoming parity bits. In this task, we will do hard decision decoding, so digitize the received voltages to get bits and then compute the Hamming distance between the expected sequence and the received sequences. That's the branch metric.

Consider using lab4.hamming(seq1,seq2) which computes the Hamming distance between two binary sequences.

viterbi_step(self,n,received_voltages)
compute self.PM[…,n] from the batch of r parity bits and the path metrics for self.PM[…,n-1] computed on the previous iteration. Follow the algorithm described above. In addition to making an entry for self.PM[s,n] for each state s, keep track of the most-likely predecessor for each state in the self.Predecessor array. You'll find the following instance variables and methods useful (scan the code to understand how to use them):

s,n = most_likely_state(self,n)
Identify the most-likely ending state of the encoder by finding the state s that has the mimimum value of PM[s,n], where n points to the last column of the trellis. If there are several states with the same minimum value, choose one arbitrarily. Return the info as a tuple (s,n).

message = traceback(self,s,n)
Starting at state s at time n, use the self.Predecessor array to trace back through the trellis along the most-likely path, determining the corresponding message bit at each time step. Note that you're tracing the path backwards through the trellis, so that you'll be collecting the message bits in reverse order -- don't forget to put them in the right order before returning the final decoded message at the result of this procedure. Hint: you can determine the message bit at each state along the most likely path from the state itself -- think about how the current message bit is incorporated into the state when the transmitter makes a transition in the state transition diagram. Be sure that your code will work for different values of self.K because we'll be testing it at least for K=3 and K=4 codes.

The testing code at the end of the template tests your implementation on a few messages and reports whether the decoding was successful or not.

When you're ready to submit your code on-line, enable the call to lab4.checkoff. When submitting, run your task file using python602 because the submission sometimes does not work correctly when run from an integrated development environment.

There are some lab questions associated with this task.

Task 4: Decoding with a soft-decision branch metric (1 point)

Let's change the branch metric to use soft decision decoding, as described in Lecture 9.

The soft metric we'll use is the square of the Euclidean distance between the received vector of dimension r, the number of parity bits produced per message bit, of voltage samples and the expected r-bit vector of parities. Just treat them like a pair of r-dimensional vectors and compute the squared distance.

lab4_4.py is the template file for this task (not shown inline here).

Complete the branch_metric method for the SoftViterbiDecoder class. Note that other than changing the branch metric calculation, the hard decision and soft decision decoders are identical. The code we have provided runs a simple test of your implementation. It also tests whether the branch metrics are as expected.

When you're ready to submit your code on-line, enable the call to lab4.checkoff. When submitting, run your task file using python602 because the submission sometimes does not work correctly when run from an integrated development environment.

There are some lab questions associated with this task.

Task 5: Comparing the performance of error correcting codes (2 points)

In this task we'll run some experiments to measure the probability of a decoding error (i.e., the bit error rate) using the codes you implemented in Tasks 2, 3, and 4 above. There's no additional code for you to write, just some results to analyze. The codes all have rate 1/2:

  1. The stream code using rectangular parity from Task 2. What should nrows and ncols be if we want a rate 1/2 code?
  2. A convolutional code with hard decision decoding and constraint length 3.
  3. A convolutional code with hard decision decoding and constraint length 4.
  4. A convolutional code with soft decision decoding and constraint length 3.
  5. A convolutional code with soft decision decoding and constraint length 4.

lab4_5.py is the template file for this task.

Run the code (please be patient, it takes a while; you can do something else while this script does its job). In the end you should see a set of plots of the probability of decoding error (the bit error rate) as a function of the amount of noise on the channel (the x axis is proportional to log(1/noise), tracking the "signal to noise ratio" (SNR) of the channel (see L9 notes for a brief explanation). Larger values of x correspond to lower noise, and a lower error probability for a given coding scheme. Note that the y axis is also on a log scale.

The Task 5 script saves the graph in a PostScript file called lab4data.ps -- during the checkoff interview, you will be asked to show this file to your TA.

End of Lab #4!

Don't forget to submit the on-line lab questions!