MIDI Controlled Sample-Based Synthesizer
Amir Hirsch and Andrew Leiserson
Sampling | MIDI | Interpolation | Filtering
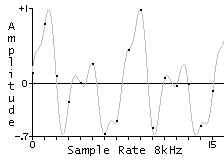
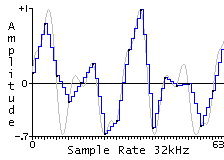
Interpolation is the process of determining continuous time values for discrete time signals. A digitally sampled recording is a set of numbers that represent the "height" of the waveform at discrete time intervals (the sampling rate for this project was 48 kHz). In order to pitch shift the sample, it must played back at a different rate (think of playing a record at a higher speed). In particular the rate you must playback the sound is equal to the ratio of the desired playback frequency to the recorded sample's frequency. For example, if the sample recorded is at frequency 220 Hz, in order to play it back at 440 Hz, you must play it back twice as fast.
However, this ratio is in most cases, not an integer value. As a result, when you try to play back the sound at a different pitch, you must figure out what the height of the waveform is at non-integer times. In order to do this we must "interpolate" the discrete-time signal. One method of interpolation involves simply rounding the non-integer time values to the nearest integer and selecting the sample at that time. The problem with this method is that the error resulting from this estimation causes a considerable amount of distortion in the output signal.
For our sampler, we used linear interpolation. A linear interpolator computes the weighted average of the two surrounding samples. For example, suppose we wanted to know the height of the waveform at sample n = 1.75. We would multiply sample 2 by .75 and sample 1 by .25 and add the results. The output is thus the weighted average. Linear interpolation is not perfect, but it is computationally cheap and it sounds relatively good compared to simply rounding. A "perfect" interpolator is called a "Bandlimited Interpolator." For information on bandlimited interpolation visit the Digital Audio Resampling Home Page.