NOTE:
You must be connected to the Internet the first time you view this simulation, at which point the codebase for all the simulations will be downloaded to your computer. This process make take a few minutes, as the codebase is roughly 9MB in size. Subsequent viewings of the applets will run from your local copy. |
|
| DESCRIPTION:
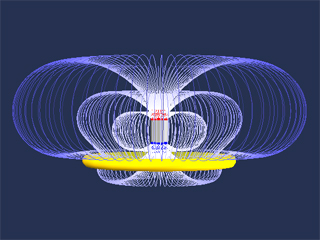
This applet shows the dynamics of a magnet falling
on the axis of a fixed conducting non-magnetic ring
. As the magnet falls under gravity towards the ring,
the changing magnetic flux through the ring gives rise
to a current which is in a direction such as to slow
the fall of the magnet, by Lenz's Law. The ring has
mass m, resistance R, and self-inductance L, and the
magnet has magnetic dipole moment M. You can vary the
resistance of the ring and the strength of the magnetic
dipole moment to see how these parameters affect
the dynamics of the magnet. If the resistance is zero
and the dipole moment is strong enough, the magnet will
levitate above the ring. If the resistance is non-zero,
even though small, the magnet will eventually fall past
the ring. We also show the induced current in the ring
in the meter on the lower left.
|
|