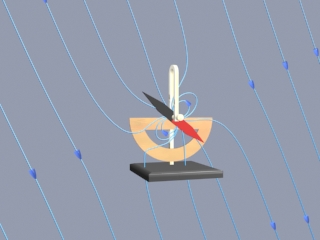
| DESCRIPTION:
A magnetic dipole in a "dip needle" oscillating
in the magnetic field of the earth, at a latitude approximately
the same as that of Boston. The magnetic field of the
earth is predominantly downward and northward at these
Northern latitudes. To explain what is going on in this
visualization, suppose that the magnetic dipole vector
is initially along the direction of the earth's field
and rotating clockwise. As the dipole rotates, the magnetic
field lines are compressed and stretched. The tensions
and pressures associated with this field line stretching
and compression results in an electromagnetic torque
on the dipole that slows its clockwise rotation.
Eventually the dipole comes to rest. But the counterclockwise
torque still exists, and the dipole then starts to rotate
counterclockwise, passing back through being parallel
to the earth's field again (where the torque goes to
zero), and overshooting. As the dipole continues to
rotate counterclockwise, the magnetic field lines are
now compressed and stretched in the opposite sense.
The electromagnetic torque has reversed sign, now slowing
the dipole in its counterclockwise rotation. Eventually
the dipole will come to rest, start rotating clockwise
once more, and pass back through being parallel to the
field, as in the beginning. If there is no damping in
the system, this motion continues indefinitely.
Faraday understood the oscillations of a compass needle
in exactly the way we describe here. In his words, "…To
understand this point, we have to consider that a [compass]
needle vibrates by gathering upon itself, because of
it magnetic condition and polarity, a certain amount
of the lines of force, which would otherwise traverse
the space about it…"
|
|