8.03 at ESG - Notes

Finding Eigenvectors using MAPLE

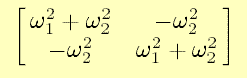
Online help is available for both Maple and Matlab:

These notes and instructions will refer to Prof. Wyslouch's lecture of September 18, 2002 (those notes are no longer available online).

If you're familiar with Maple, or would rather figure out for yourself what to do (a common feature of MIT students), the worksheet may be downloaded here (you must download Maple worksheets with the right mouse button, or Shift-left button).

To start Maple from an Athena terminal, either start from the dash, or, at the Athena prompt, do

athena% add maple
athena% maple&

Now, wait. Maple, like MATLAB, takes a while to load. Also like MATLAB, the older versions load and run faster (go figure). To load an older release, the command is
athena% maple -ver 5r3&
(the commands given here will run on the older releases).
If you've downloaded the worksheet, or have your own, you open these from the File menu item.

The Maple prompt is >. All commands to be executed must end with a semicolon (;) followed by a return. For linebreaks within a command, do Shift-return.
All of the commands given here (in ``keyboard'' or ``teletype'' font) may be copied directly from this page and pasted into your Maple session (this turns out to be browser-dependent).

First, load the ``Linear Algebra'' package with

with(linalg);

This will give you some idea of what Maple can do, although if you're not familiar with the terms, you might satisfy your curiosity by searching for the commands from the Help window.

Next, define a matrix, starting with, for instance the matrix

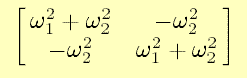
(note that the subscripts 1 and 2 are used instead of 0 and s, which were used in lecture).

To enter this as a matrix, the command would be

A1:=matrix([[omega1^2+omega2^2,-omega2^2], [-omega2^2,omega1^2+omega2^2]]);

Remember, if you want a linebreak within a command, it's Shift-return. Note that the labels ``1'' and ``2'' on the frequencies do not show up a subscripts. Deal with it.

To find the eigenvalues of the matrix we've called A1, the command is

eigenvals(A1);

The eigenvalues thus obtained were those found in lecture, corresponding to the mode where the spring is not strecthed (the symmetric mode) and the mode where the spring is stretched the same on both sides (the antisymmetric mode).
The eigenvectors are found with

eigenvects(A1);

What's returned from this command needs explaining. What we get is two sets, within [square braces]. Each set consists of the eigenvalue, the multiplicity of the eiqenvalue, and the set of eigenvectors corresponding to each eigenvalue. In this case, there are no repeated eigenvalues (the quadratic equation obtained from finding the determinant, known as the characteristic equation, has no repeated roots), and each eigenvalue has only one associated eigenvector. The set of eigenvectors is enclosed in {curly braces} and the component of each eigenvector is in turn enclosed in [square braces]. You should recognize these eigenvectors as those found in lecture.
(As an aside, try entering the 2×2 identity matrix, called A4 in the worksheet if you've downloaded, and see what you get.)

You've certainly noticed that if you want both the eigenvalues and the eigenvectors, the eigenvals(A1) command is redundant. It's your choice.

Next, try the 3×3 matrix for the three identical masses coupled by identical springs, with the command

A2:=matrix([[2*omega0^2,-omega0^2,0],[-omega0^2,2*omega0^2,-omega0^2], [0,-omega0^2,2*omega0^2]]);

You should obtain the matrix

.

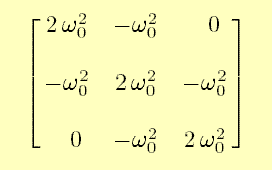The command

eigenvects(A2);

gives the expected result, except that in two of the eigenvectors, the common factor has not been canceled. This is because Maple is too smart for its own good; if this common factor were zero, which is not precluded on mathematical grounds, the results might be interpreted differently.

One way around this is for us to do the math beforehand, basically factoring out any common term. This also makes it easier to enter the matrix as

A3:=matrix([[2,-1,0],[-1,2,-1],[0,-1,2]]);

and of course the command

eigenvects(A3);

gives the simpler result.

Another useful technique is to extract the desired value and simplify. In this case, the output of the eigenvects(A2) command is a nested set of lists, and the command

r2:=s1[2][3][1][2];

isolates the desired component. From that,

simplify(r2);

gives the simplification.

A word of caution for those already looking at the next Problem Set; if the masses were different, you would have to do something different to your matrices in order to consder the (squared) frequencies as eigenvalues, and it turns out that the term ``normal modes'' has a slightly different interpretation.
This page was written rather quickly; suggestions or comments, including notice of errors of any kind, would be greatly appreciated. Send to Craig Watkins.
Back to the 8.03-ESG page.