|
FORWARD |
Random Walks and Plasmas
We have described two fields that seem to have nothing to do with
each other. However this is far from being true. The topic of this last section
will be to show how random walks can prove useful in Plasma Physics. We should
warn the reader that this is a rather technical matter, so we will try only to
sketch some basic features of it.

Let’s suppose that
the starting point and the ending point of a random walk are separated by a
distance r(t). We now consider the mean square displacement, which is
proportional to some power of the lapsed time t, that is ![]() .
.
Anomalous
diffusion is characterized by the exponent ã, which define the nature of the walk as
follows
·
ã=1: classical diffusion
·
ã>1: super-diffusion (in the special case ã=2, ballistic diffusion)
·
ã<1: sub-diffusion
Anomalous diffusion
can lead to statistical properties of plasmas, such as density and temperature
profiles exhibiting anomalous (which means strange or unexpected) behavior.
Some examples
effects caused by anomalous diffusion:
·
Profile
stiffness, meaning that the density or temperature profile stays close to a
certain shape, even if the plasma is distorted
·
Cooling
at the edge can lead to a temperature rise at the center
·
During
heating at the edge, there can be an inward electron heat flux, in direction of
increasing temperature (so-called “uphill” transport of energy
·
Sudden
cooling at the edge may lead to a temperature drop that propagates inwards with
constant velocity (![]() , super-diffusion)
, super-diffusion)
In a turbulent
plasma, a particle can freely travel along the magnetic field lines, drift
across the magnetic field lines, be locally trapped or locally accelerated.
Turbulence
implies complex spatiotemporal structures, where each individual particle
performs a random walk!
So does it work?
YES! It has been shown that Random Walk can successfully model
observed phenomena of anomalous transport in confined plasmas, such as profile
stiffness and uphill transport.
The final
food for thought.
Uses of random
in describing the above phenomena can be found in the following papers
Montroll, E.W.
Weiss, G.H, J. Math. Phys. 6, 167 (1965)
Balescu, R., Phys. Rev. E 51, 4807 (1995)
Van Milligen, B.Ph., Sanchez, R., Carreras, B.A., PoP 11,
2272 (2004)
Van Milligen, Carreras, B.A., B.Ph., Sanchez, R., PoP 11,
3787 (2004)
Finally, we must
mention the Fokker-Planck equation, which follows from Browninan motion and was
first used to describe the motion of a particle in a fluid (also a plasma). The
Fokker Planck equation is the major link between plasmas and random walks,
however we just mention it now, since we wanted to present some new
developments in the subject.
Without proving
it, the 1-D Fokker Planck equation for some process f(x,t) with drift D1(x,t)
and diffusion D2(x,t) is
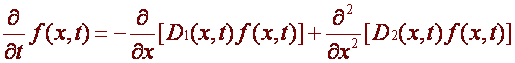
THE END