It’s all nice,
but can we do anything else with it?
Sure we can! I
must warn you though, things start to get complicated and technical, so for those
that are willing to hear a bunch of terms and see a couple of definition, this
will be all there is to it!
· Stochastic Integral
Sometimes it is
useful to define integrals over the increments of Brownian motion, that is
quantities of the form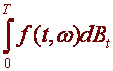 
.
Here f(t,ù) is a random variable and dBt
is the increment of the Brownian motion in the interval from t to t+dt.
Unfortunately
this integrals inherits the pathogenic behavior of Brownian motion, so there is
a need for a new definition
The problem was
solved by Ito, who defined what is today known as “Ito integral”, which follows
a somewhat strange calculus, as compared to the usual Riemann integral.
As an example,
using Ito’s integral we will get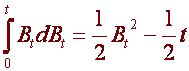 
,
where the second
term shows the difference from what we would expect from our usual rules of
integration!
· Stochastic differential equations
A stochastic
differential equation is an equation of the form 
Or in integral
form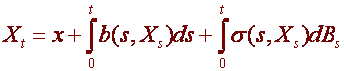 
, where Bt
is a Brownian motion.
The two
hypotheses we have to make for b and ó are the following
o
Lipschitz
continuity
o
Linear
growth condition
An important
example is the Ornstein-Uhlenbeck process 
, which has important
applications in physics, as a particle subject to a stochastic force and a
friction analogous to is velocity.
However, the
whole structure emanating from Brownian motion is not restricted to physics,
but is also extended to other areas, from biology to finance!
Food for
thought!
For those who
didn’t suffer enough, here are two books on the subject:
“Basic Stochastic
Processes” by Brzezniak and Zastawniak
“Stochastic
Differential Equations” by B. Oksendal (more mathematically challenging than
the above)
Is there
anything left?
Of course! The
title is “Plasmas and Random Walks”. So far we talked a bit about both. But the
connection remains unseen!
As a closing
remark, I will present VERY briefly one connection between the two.