Plasma Oscillations and Landau Damping
We know all
about plasma oscillations: A longitudinal wave comes in, the electric field is
parallel to the direction of propagation, the electrons move back and forth and
thus the wave moves through the plasma forever.
Right? Wrong!
What we didn’t
talk about is the so-called thermal motion of the electrons.
So far we acted
as if the electrons are at rest before the appearance of the wave. But this is
not true! The electrons have a random motion, just like atoms and molecules in
an ordinary gas. They move around, and statistically the number of electrons
gets smaller, as the velocity gets higher (keep that in mind)
In the following
picture, we show the potential created by a longitudinal wave (because of
charge density distribution, as explained before)
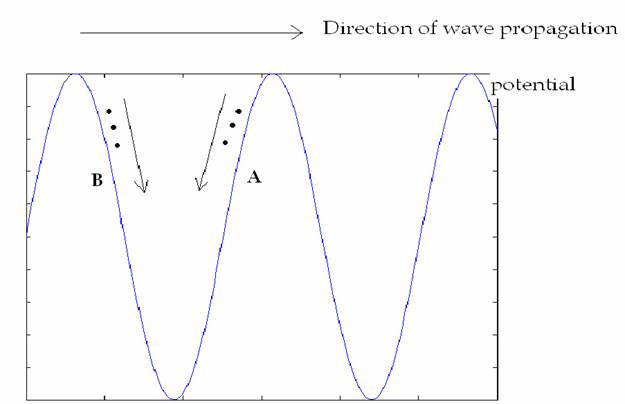
The particles
that move with the same velocity as the wave, will always see a constant
potential (resonance).
Those particles
that move slightly faster than the wave, will be decelerated, so part of their
kinetic energy (since it cannot be lost) will be given to the wave (case A of
the above figure).
Those particles
that move slightly slower than the wave, will be accelerated, so they will take
energy from the wave and turn it into kinetic energy (case B of the above
figure).
We said that the
particles with smaller velocities are more than the particles with larger
velocities!
So overall the
wave will give away MORE energy than it will gain! This means that the wave
will be attenuated, as it travels through the plasma!
This phenomenon
is known as “Landau Damping”
We are now
experts in longitudinal waves. What else is there?
But transverse
waves of course! Do you remember the term? Transverse waves have their electric
and magnetic fields perpendicular to the direction of wave propagation. Now the
real wave zoo appears! There is a whole bunch of different cases of waves, but we
will just mention some of them, which can be explained without cumbersome math,
and can give you a feeling about plasmas.