TRANSVERSE
WAVES IN PLASMAS
Letís start by
remembering what we know about waves in general, such as a wave on a guitar
string. We know that the displacement of the string from its equilibrium
position is proportional to sin(kx-ýt), as shown below
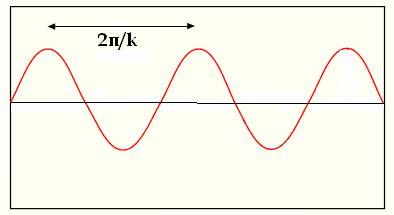
The relation
between the frequency ý and
the wavenumber k is called ďdispersion relationĒ and is characteristic of the
medium, where the wave propagates. For E/M waves in vacuum we know that ý=ck.
So, what happens
if we try to send a transverse electromagnetic wave through a plasma?
First we have to
define the properties of the plasma!
First of all, it
is an electron-ion plasma with equal density (so it is overall neutral)
Because of their
high mass, we consider the ions as static, so everything is determined by the
motion of the electrons.
There is no
constant magnetic field present (unmagnetized plasma) and we neglect the
thermal motion of the electrons (cold plasma).
Under the above
assumptions, the dispersion relation that can be calculated is presented in the
figure below
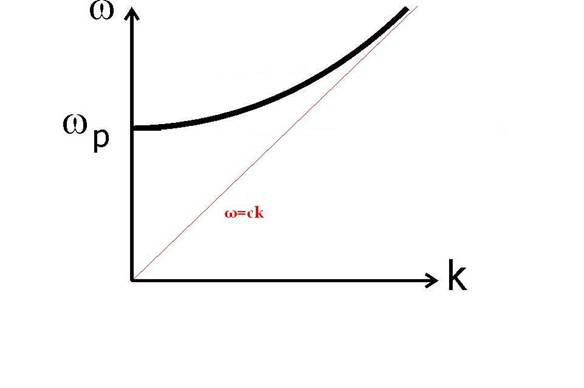
Letís see what
this means!
First of all, we
see that as the frequency gets higher, the graph tends to become the vacuum
relation ý=ck. Is this
understandable?
Of course, this
should be anticipated. Due to their inertia, as the changes in the field happen
faster and faster, the electron become unable to follow them, so the wave goes
through plasma as if it werenít there!
On the other end,
we see that there is nothing below, a certain value, which is our old friend
the Plasma frequency!
What happens
there? Any wave that is below that frequency cannot propagate in the plasma,
and is therefore REFLECTED.
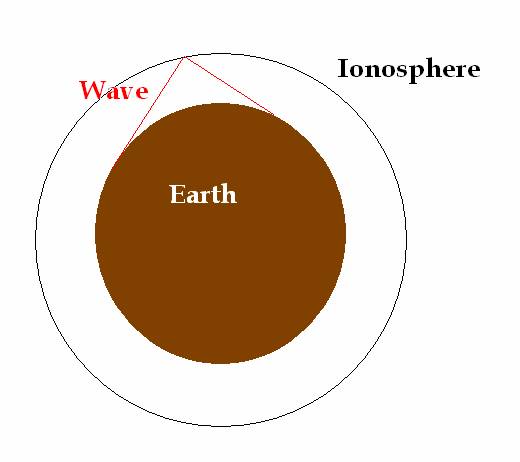
Sounds familiar?
Well, it should. Remember the old days, when people used to bounce radiowaves
off the ionosphere? Thatís how they did it! If you use a frequency that is
lower than the plasma frequency for the ionospheric plasma, the radiowaves will
be reflected. That way, one can beat the curvature of the earth and transmit
signals in large distances.
However nowadays
we have satellites, so we do not want the ionosphere to reflect our signals!
Easy again! We
use a high enough frequency, so that the wave practically ignores the existence
of the ionospheric plasma!
We see that with
a simplified model, we can understand a lot about modern telecommunications!