If a man talks in the forest and his wife is not there to hear him, is he still wrong?

A couple moved to a new city in which they didn't know anyone. In order to meet people they placed an ad in the local newspaper asking married couples between the ages of 20 to 40 to come on Friday at 8 PM to their house for a party.

On Friday at 8, 4 couples came to their house, making it a total of 10 people in the party (including the hosts). None of the people knew anyone at the party but their own spouse.

The host asked all the people in the party to walk to new people, introduce themselves, and shake their hand. After a few minutes the host asked everyone to stop and tell him how many hands did they shake.

He got 9 answers (all the others but himself) that were all different from each other (0, 1, 2, 3, 4, 5, 6, 7, 8). The questions is: How many hands did his wife shake? Another question would be how many hands did the host himself shake?

A couple lives in city A and the wife works in city B (the husband works at home). Every day the wife takes the bus at 4 PM back from city B to city A and the husband comes to pick her at the bus station and they go home (it is unknown when she gets to city A but it is in the same time every day).

The husband is so good in timing this that he knows exactly when to leave home in order to pick his wife at the exact time that she gets off the bus in city A.

One day the wife took the bus at 3 instead of 4 and as a consequence got to city A an hour before the regular time. It was a nice day so she decided not to call her husband but to start walking in the direction of their house.

Her husband didn't know anything about this and left at his regular time to pick her up. On the way to the bus station he saw her, picked her up and they both returned home 20 minutes earlier than usual.

The question is: How long did the wife walk before she was picked up?

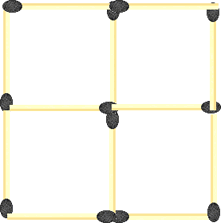
By repositioning only two of the matches in the following picture, how would you create four squares instead of 5? (remember they have to be repositioned).

Two Chinese men meet on the street. The first asks the second how his family is, and the second answers: "They're great. I have three sons. They all have their birthday today. The sum of their ages is 13. The product of their ages is the number that house across the street."

The next day they meet again, and the first man tells the second: "I almost have it, but I need one more piece of information before I can tell you how old your children are." The second answers: "Oh, my oldest son plays the violin." The first man says: "Okay, I've got it."

The question is, how old are the children?

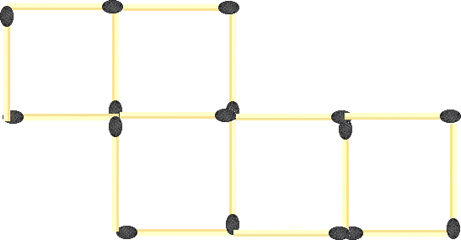
By repositioning only three of the matches in the following picture, how would you create three squares instead of 4? (remember they have to be repositioned).