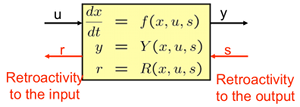
|
The assumption that is usually made when designing or analyzing a network modularly is that the input/output behavior of a module does not change upon interconnection. We have discovered that, just as in many electrical, mechanical, and hydraulic systems, this assumption is not satisfied in biomolecular systems. Specifically, upon interconnection of a biomolecular component with a downstream system, “impedance-like” effects arise, which alter the behavior of the upstream component. We have called these effects retroactivity, to extend the notion of impedance to non- electrical circuits and in particular to biomolecular systems. We are developing a network theory based on retroactivity that seeks to determine retroactivity to the input and to the output of any general network. This Will allow to reliably predict the behavior of complex Interconnected networks from the behavior of their “modules”, Just like Thevenin’s theorem does in electrical circuits. We experimentally validate our hypothesis by constructing test Circuits in E coli to measure retroactivity� |
Retroactivity�
Design of Insulation devices�

|
To modularly design biomolecular circuits, retroactivity must be counteracted. To this end, we have proposed to place insulation devices between an upstream system sending the signal and a downstream system receiving the signal to buffer them from retroactivity effects. An insulation device is designed to act like an isolation amplifier: it has almost zero retroactivity to the input and almost completely attenuates the retroactivity to the output. We are designing these molecular devices based on control-theoretic notions of disturbance attenuation and we have been identifying naturally occurring signaling modules that can implement this new isolation function: covalent modification cycles. Our work is both theoretical and experimental as we build our designs in E coli cells. |
Demand and adaptation of cellular resources�
|
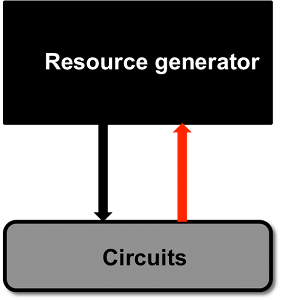
One fundamental question when inserting a synthetic circuit in the cellular chassis is how it is going to alter the cellular environment and, with it, other synthetic circuits that are already present in the cell. In fact, all circuits, for their functioning, employ shared cellular resources such as RNA polymerases and ribosomes, and hence there is competition for shared resources. On the one hand, this may hinder cell growth, on the other hand, this may create unwanted crosstalk among “unconnected” circuit components. We perform mathematical studies and simple experiments in E coli to characterize this problem. At the same time, we investigate designs for adaptation to changing demands by employing control-theoretic tools, such as integral feedback and the internal model principle. � |
Analysis and design of stochastic biomolecular systems�
|
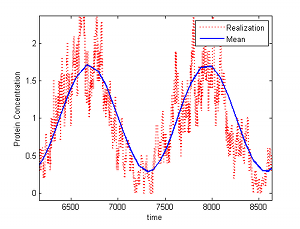
Biomolecular systems are intrinsically stochastic. Therefore, It is important to understand the repercussions of any design (for example for insulation or adaptation) on the noise of the system. For example, the high gains that are at the basis of some insulation device designs may enhance noise. In order to understand stochastic effects, it is essential to reduce the complexity of the system to obtain an analytical grasp. A powerful tool in deterministic systems to reduce the complexity of a model is exploiting time-scale separation, which is ubiquitous in biomolecular systems. To perform this model reduction, we are developing a singular perturbation theory for stochastic systems modeled by the master equation. Concurrently, we are employing these techniques to obtain insights on the stochastic effects of retroactivity and insulation and to investigate possible fundamental limitations. � |