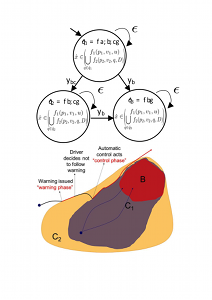
In this project, we consider the safety control problem for Hidden Mode Hybrid Systems (HMHSs), which are a special class of hybrid automata in which the mode is not available for control. For these systems, safety control is a problem with imperfect state information. We are tackling this problem by introducing the notion of non-deterministic discrete information state and by translating the problem to one with perfect state information. The perfect state information control problem is obtained by constructing a new hybrid automaton, whose discrete state is an estimate of the HMHS mode and is, as such, available for control. This problem is being solved by computing the capture set (the complement of the maximal controlled invariant set) and the least restrictive control map for the new hybrid automaton. Termination of the algorithms that compute the capture set is also investigated. The theory is being applied to the development of on-board driver assist systems that prevent collisions at intersections, merges, and roundabouts.

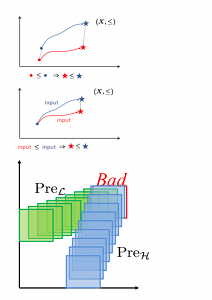
Computing safety controllers with imperfect information is usually computationally prohibitive for general systems. In order to overcome this bottleneck, we have restricted the class of systems to those whose state spaces and inputs can be extended to partial orders (lattices) and whose trajectories preserve the partial ordering on the state space (Figure on the top left). Specifically, we have shown using lattice theory that in such a case, the complexity of the hybrid state estimator can be linear with the number of variables and that convergence is guaranteed under suitable observability assumptions. Furthermore, the proposed dynamic feedback algorithm can also have linear complexity with the number of continuous variables. This is because the computations of the capture sets reduce to the computation of suitable upper and lower bounds (Figure on the bottom left). A number of systems of practical relevance generate trajectories that preserve a partial ordering. Examples include multi-agent systems in which agents evolve on paths, such as vehicles in lanes, trains on rails, and aircrafts on their pre-designed routes, as well as several bio-molecular and chemical networks. We are currently extending these techniques to apply to general systems for which an order preserving abstraction can be computed.

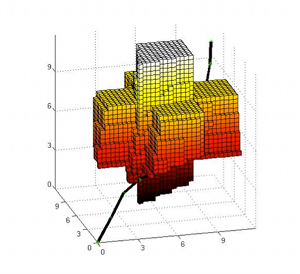
The limiting factor in most implementations of safety enforcing controllers is the model’s complexity, and a common work-around includes the abstraction of the physical model, based on differential equations, to a finite symbolic model. We exploit the specific structure of a class of systems (the differentially flat systems) to perform the abstraction. The objective is to construct a supervisor enforcing a set of safety rules, while imposing as little constraints as possible on the system’s functionality. We are applying these techniques to cooperative active safety systems and to systems of robotic manipulators with impacts, such as crane systems. We are currently extending these techniques to the case of imperfect state information and to more general dynamics.

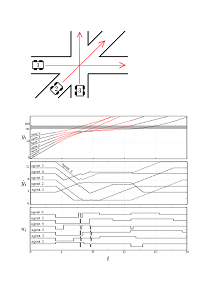
We consider the problem of synthesizing the least restrictive controller for collision avoidance of multiple vehicles at an intersection. The largest set of states for which there exists a control that avoids collisions is known as the maximal controlled invariant set. Exploiting results from the scheduling literature we prove that, for a general model of vehicle dynamics at an intersection, the problem of checking membership in the maximal controlled invariant set is NPhard. We investigate algorithms that solve this problem approximately and with provable error bounds for systems with Perfect and imperfect information. The approximate solution is used to design a supervisor for collision avoidance whose complexity scales polynomially with the number of vehicles. The supervisor is based on a hybrid algorithm that employs a dynamic model of the vehicles and periodically solves a scheduling problem.

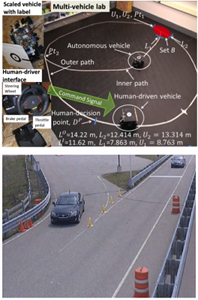
We are currently validating our algorithms on fully autonomous cooperative active safety systems to prevent collisions at intersections and on semi-autonomous (driver-assist) systems. We perform testing both in out multi-vehicle lab (Figure top left) and on full-scale vehicles equipped with wireless communication, automatic throttle, and automatic braking capability